E. Hoạt động vận dụng và tìm tòi, mở rộngCâu 1: Trang 162 toán VNEN 9 tập 2Hình 194 bao gồm hai...
Câu hỏi:
E. Hoạt động vận dụng và tìm tòi, mở rộng
Câu 1: Trang 162 toán VNEN 9 tập 2
Hình 194 bao gồm hai phần. Phần phía trên là nửa hình cầu có bán kính 21 cm. Phần phía dưới là hình nón cụt có bán kính hai đáy là 9 cm và 21 cm, đường sinh là 40 cm. Tính diện tích xung quanh và thể tích của hình này.
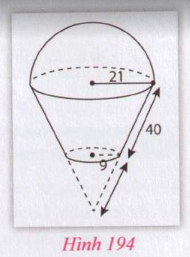
Câu trả lời:
Người trả lời: GV. Đỗ Văn Huy
Câu trả lời đầy đủ và chi tiết cho câu hỏi trên như sau:Đầu tiên, chúng ta cần tính đường cao của hình nón cụt:Đường cao của hình nón cụt là: $h = \sqrt{l^2 - (r_1 - r_2)^2} = \sqrt{40^2 - (21-9)^2} = 4\sqrt{91}$ cmTiếp theo, tính diện tích xung quanh và thể tích của hình nón cụt:Diện tích xung quanh hình nón cụt:$S_{xq1} = \pi \times (r_1 + r_2)\times l = \pi \times (9 + 21)\times 40 = 1200\pi \; cm^2$Thể tích hình nón cụt:$V_1 = \frac{1}{3} \pi \times h\times (r_1^2+r_2^2+r_1\times r_2) = \frac{1}{3} \pi \times 4\sqrt{91}\times (9^2+21^2+9\times 21) = 948\sqrt{91}\pi \; cm^3$Sau đó, tính diện tích xung quanh và thể tích của nửa hình cầu:Diện tích xung quanh nửa hình cầu:$S_{xq2} = \frac{1}{2}\times 4\pi \times r^2 =\frac{1}{2}\times 4\pi \times 21^2 = 882 \pi \; cm^2$Thể tích nửa hình cầu:$V_2 = \frac{1}{2}\times \frac{4}{3} \pi \times r^3 = \frac{1}{2}\times \frac{4}{3} \pi \times 21^3 = 6174\pi \; cm^3$Cuối cùng, tính diện tích và thể tích của toàn bộ vật:Diện tích tổng cộng:$S = S_{xq1} + S_{xq2} = 1200\pi + 882\pi = 2082\pi \; cm^2$Thể tích tổng cộng:$V = V_1 + V_2 = (948\sqrt{91}\pi + 6174\pi) = (948\sqrt{91} + 6174)\pi \; cm^3$Vậy, diện tích xung quanh của hình này là 2082π cm^2 và thể tích của hình này là (948√91 + 6174)π cm^3.
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 159 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại các...
- Câu 2: Trang 159 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại các kiến thức, kĩ năng đã...
- Câu 3: Trang 160 toán VNEN 9 tập 2Em hãy điền vào ô trống trong bảng sauĐường cao của hình trụh = 3...
- Câu 4: Trang 160 toán VNEN 9 tập 2Em hãy điền vào ô trống trong bảng sauBán kính đáy của hình nónr...
- Câu 2: Trang 162 toán VNEN 9 tập 2Một cái xúc xích có dạng hình trụ bán kính 1,2 cm. Nếu dùng dao...
- Câu 5: Trang 162 toán VNEN 9 tập 2Vật thể ở hình 193 gồm 3 phần. Phần dưới cùng là hình nón chiều...
- Câu 4: Trang 161 toán VNEN 9 tập 2Tính thể tích của vật thể trong hình 192, biết rằng phần vật thể...
- Câu 3: Trang 161 toán VNEN 9 tập 2Quả cầu thép có dạng hình cầu, bán kính bằng 2 m. Tính khối lượng...
- Câu 2: Trang 161 toán VNEN 9 tập 2Một ống thép bề ngoài có mặt dạng xung quanh hình trụ, bán kính...
- D. Hoạt động vận dụngCâu 1: Trang 161 toán VNEN 9 tập 2Một củ cà rốt sau khi gọt có dạng một hình...
- Câu 7: Trang 161 toán VNEN 9 tập 2Em hãy điền vào ô trống trong bảng sauBán kính của hình cầur = 3...
- Câu 6: Trang 161 toán VNEN 9 tập 2Em hãy điền vào ô trống trong bảng sauĐường sinh của hình nón...
- Câu 5: Trang 160 toán VNEN 9 tập 2Em hãy điền vào ô trống trong bảng sauĐường cao của hình nón...






Tổng diện tích xung quanh của hình này là S_total = S_cone + S_hemisphere = 1130.97 + 2776.38 = 3907.35 cm². Thể tích của hình này được tính bằng công thức V = (1/3)πr²h cho hình nón và V = (2/3)πr³ cho nửa hình cầu. Tổng thể tích của hình là V_total = V_cone + V_hemisphere = (1/3)π*9²*40 + (2/3)*π*21³ = 43276.19 cm³.
Diện tích xung quanh của nửa hình cầu là: S = 2πr², với r là bán kính. Substituting r = 21 cm, we have S = 2*π*21² = 2776.38 cm².
Diện tích xung quanh của hình nón cụt là: S = πr*l, với r là bán kính đáy nhỏ, l là đường sinh. Substituting r = 9 cm, l = 40 cm, we have S = π*9*40 = 1130.97 cm².