E. HOẠT ĐỘNG TÌM TÒI, MỞ RỘNGHình vành khuyên kì lạLấy hính vành khuyên có kích thước bất kì tạo...
Câu hỏi:
E. HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG
Hình vành khuyên kì lạ
Lấy hính vành khuyên có kích thước bất kì tạo bởi hai hình tròn đồng tâm, phần màu hồng (hình 138). Bạn có chứng minh được rằng diện tích của hình vành khuyên bằng diện tích của hình tròn có đường kính là dây cung của vòng tròn lớn nhưng lại là tiếp tuyến của đường tròn nhỏ?
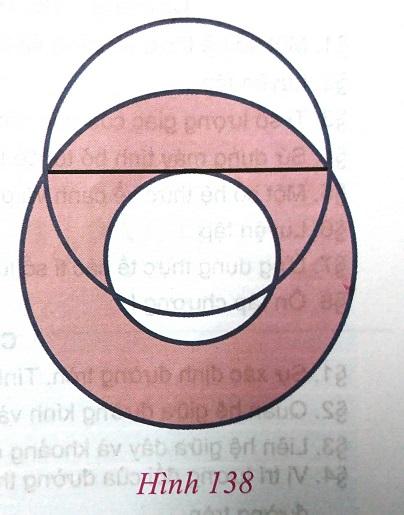
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ngọc
Cách làm:1. Vẽ hình và đặt tên các điểm như trong hình vẽ.2. Tính diện tích của hình vành khuyên bằng cách trừ diện tích của hình tròn lớn cho diện tích của hình tròn nhỏ.3. So sánh diện tích đó với diện tích của hình tròn có đường kính là dây cung của vòng tròn lớn.Câu trả lời:Diện tích của hình vành khuyên là S = πR^2 - πr^2 = π(R^2 - r^2) = π(HB^2)Diện tích của hình tròn có đường kính là AB là S' = πHB^2Do đó, S = S'Vậy diện tích của hình vành khuyên bằng diện tích của hình tròn có đường kính là dây cung của vòng tròn lớn nhưng lại là tiếp tuyến của đường tròn nhỏ.
Câu hỏi liên quan:
- Câu 1: Trang 129 sách VNEN 9 tập 1Cho tam giác đều ABC cạnh bằng 2cm. Bán kính của đường tròn ngoại...
- Câu 2: Trang 129 sách VNEN 9 tập 1Xét tính đúng - sai của mỗi khẳng định sau:Cho$\Delta $ABC...
- Câu 3: Trang 129 sách VNEN 9 tập 1Độ dài cạnh của tam giác đều nội tiếp (O; R)...
- Câu 4: Trang 129 sách VNEN 9 tập 1Cho đường tròn (O) đường kính 10cm, dây AB = 6cm. Khoảng cách từ...
- Câu 5: Trang 129 sách VNEN 9 tập 1Cho hình 137:Trong đó OA = 3cm, O'A = 2cm, AM = 5cm.Độ dài AN...
- Câu 6: Trang 130 sách VNEN 9 tập 1Cho (O; R) và (O'; r). Điền vào chỗ chấm (...) của bảng...
- Câu 7: Trang 130 sách VNEN 9 tập 1Tỉ số bán kính của đường tròn nội tiếp, đường tròn ngoại tiếp của...
- D. HOẠT ĐỘNG VẬN DỤNGCâu 1: Trang 130 sách VNEN 9 tập 1Cho đường tròn (O) có đường kính AB. Từ điểm...
- Câu 2: Trang 130 sách VNEN 9 tập 1Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp...
- Câu 3: Trang 131 sách VNEN 9 tập 1Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại A và B (R >...






Dựa vào tính chất của hình vành khuyên, ta có thể chứng minh rằng diện tích của hình vành khuyên bằng diện tích của hình tròn có đường kính là dây cung của vòng tròn lớn nhưng lại là tiếp tuyến của đường tròn nhỏ.
Diện tích của hình vành khuyên bằng diện tích của hình tròn lớn trừ đi diện tích của hình tròn nhỏ.
Để chứng minh điều này, ta có thể sử dụng công thức tính diện tích của hình vành khuyên.