Câu 5: Trang 33 sách toán VNEN lớp 9 tập 2Biết rằng đường cong trong hình 9 là một parabol $y =...
Câu hỏi:
Câu 5: Trang 33 sách toán VNEN lớp 9 tập 2
Biết rằng đường cong trong hình 9 là một parabol $y = ax^2 (a\neq 0)$
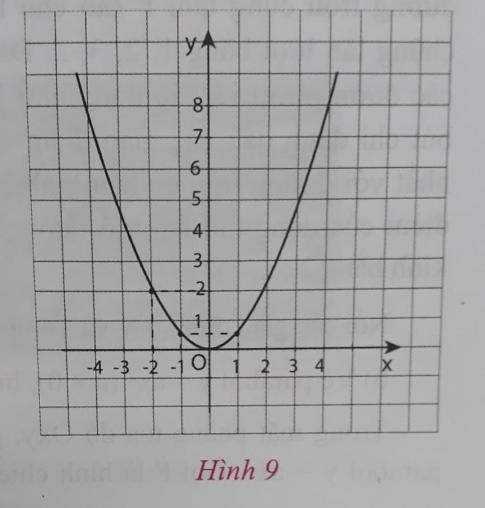
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol và có hoành độ x = -3.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Phương
a) Để tìm hệ số a, ta sử dụng điểm thuộc parabol là (-2; 2):$2 = a\times (-2)^2 \Rightarrow a = \frac{1}{2}$b) Để tìm tung độ của điểm có hoành độ x = -3, ta thay x = -3 vào phương trình parabol:$y = \frac{1}{2}(-3)^2 = \frac{9}{2}$c) Để tìm hoành độ của các điểm có tung độ y = 8, ta giải phương trình $8 = \frac{1}{2}x^2$:$x = \pm \sqrt{2y} = \pm \sqrt{2\times 8} = \pm 4$Vậy câu trả lời đầy đủ và chi tiết hơn sẽ là: a) Hệ số a của parabol là $\frac{1}{2}$.b) Tung độ của điểm có hoành độ x = -3 là $\frac{9}{2}$.c) Các điểm thuộc parabol có tung độ y = 8 là (-4; 8) và (4; 8).
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 32 sách toán VNEN lớp 9 tập 2Cho hàm số: $y =...
- Câu 2: Trang 32 sách toán VNEN lớp 9 tập 2Cho ba hàm số: $y = -\frac{1}{2}x^2;\;y=-x^2;\;y = -2x^2...
- Câu 3: Trang 33 sách toán VNEN lớp 9 tập 2Cho đồ thị hàm số $ y = f(x) = x^2$a) Vẽ đồ thị hàm sốb)...
- Câu 4: Trang 33 sách toán VNEN lớp 9 tập 2Trên mặt phẳng tọa độ (hình 8) có điểm M(2; 1) thuộc đồ...
- Câu 6: Trang 34 sách toán VNEN lớp 9 tập 2Cho hai hàm số $y = -\frac{1}{3} x^2$ và $y = x - 6$a) Vẽ...
- D. E Hoạt động vận dụng và tìm tòi, mở rộngCâu 1: Trang 34 sách toán VNEN lớp 9 tập 2Cho hàm số $y...
- Câu 2: Trang 34 sách toán VNEN lớp 9 tập 2Cho hàm số $y = ax^2 (a\neq 0)$a) Tìm a, biết rằng đồ thị...






f) Sau khi có hoành độ x, ta có thể tính tung độ của các điểm thuộc parabol bằng cách thay giá trị của x vào phương trình parabol y = ax^2.
e) Tìm các điểm thuộc parabol có tung độ y = 8: Thay y bằng 8 vào phương trình parabol y = ax^2 và giải phương trình để tìm ra các hoành độ x tương ứng.
d) Tìm tung độ của điểm thuộc parabol và có hoành độ x = -3: Tính y theo công thức y = a*(-3)^2
c) Tung độ của điểm thuộc parabol với hoành độ x = -3: Ta đã tính được hệ số a ở câu b), nên ta có y = a*(-3)^2 = a*9
b) Tính hệ số a: Với hoành độ x = -3, ta có y = a*(-3)^2 => y = 9a. Do đó, hệ số a = y/x^2 = 9a / (-3)^2 = 9a/9 = a