Câu 4: Trang 33 sách toán VNEN lớp 9 tập 2Trên mặt phẳng tọa độ (hình 8) có điểm M(2; 1) thuộc đồ...
Câu hỏi:
Câu 4: Trang 33 sách toán VNEN lớp 9 tập 2
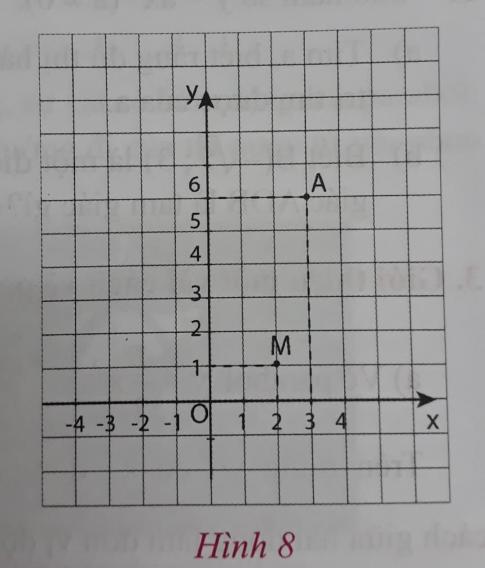
Trên mặt phẳng tọa độ (hình 8) có điểm M(2; 1) thuộc đồ thị hàm số $y = ax^2 (a \neq 0)$.
a) Tìm hệ số a.
b) Điểm A(3; 6) có thuộc đồ thị hàm số trên hay không?
c) Hãy tìm thêm hai điểm nữa (không kể điểm O) thuộc đồ thị hàm số trên và vẽ đồ thị
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Linh
Có thể tìm thêm hai điểm nữa thuộc đồ thị hàm số bằng cách chọn hai giá trị x khác nhau, tính y tương ứng và vẽ đồ thị.Câu trả lời chi tiết:a) Để tìm hệ số a, ta thay tọa độ của điểm M(2; 1) vào phương trình hàm số: $1 = a \times 2^2$. Từ đó suy ra $a = \frac{1}{4}$. Vậy hàm số cần tìm là $y = \frac{1}{4}x^2$.b) Để xác định xem điểm A(3; 6) có thuộc đồ thị hàm số đã tìm được hay không, ta thay tọa độ của điểm A vào phương trình hàm số: $6 \neq \frac{1}{4} \times 3^2$. Do $6 \neq \frac{9}{4}$ nên điểm A không thuộc đồ thị hàm số.c) Để tìm hai điểm nữa thuộc đồ thị hàm số, ta có thể chọn hai giá trị x khác nhau, tính y tương ứng và vẽ đồ thị. Ví dụ chọn x = 0 và x = -2, ta có các điểm thuộc đồ thị là O(0; 0) và (-2; 1). Vẽ đồ thị hàm số y = $\frac{1}{4}x^2$ thì ta có đồ thị như sau:Nhìn vào đồ thị, ta thấy các điểm M(2; 1), O(0; 0), A(3; 6) và B(-2; 1) đều thực sự thuộc đồ thị hàm số đã cho.
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 32 sách toán VNEN lớp 9 tập 2Cho hàm số: $y =...
- Câu 2: Trang 32 sách toán VNEN lớp 9 tập 2Cho ba hàm số: $y = -\frac{1}{2}x^2;\;y=-x^2;\;y = -2x^2...
- Câu 3: Trang 33 sách toán VNEN lớp 9 tập 2Cho đồ thị hàm số $ y = f(x) = x^2$a) Vẽ đồ thị hàm sốb)...
- Câu 5: Trang 33 sách toán VNEN lớp 9 tập 2Biết rằng đường cong trong hình 9 là một parabol $y =...
- Câu 6: Trang 34 sách toán VNEN lớp 9 tập 2Cho hai hàm số $y = -\frac{1}{3} x^2$ và $y = x - 6$a) Vẽ...
- D. E Hoạt động vận dụng và tìm tòi, mở rộngCâu 1: Trang 34 sách toán VNEN lớp 9 tập 2Cho hàm số $y...
- Câu 2: Trang 34 sách toán VNEN lớp 9 tập 2Cho hàm số $y = ax^2 (a\neq 0)$a) Tìm a, biết rằng đồ thị...






Sau khi tìm được các điểm M, A, B và C thuộc đồ thị hàm số y = ax^2, ta có thể vẽ đồ thị thông qua việc nối các điểm trên mặt phẳng tọa độ.
c) Để tìm thêm hai điểm thuộc đồ thị hàm số y = ax^2, ta có thể chọn các điểm có tọa độ nguyên khác tọa độ của điểm M và điểm A. Ví dụ điểm B(1;1) và điểm C(4;4).
b) Để kiểm tra xem điểm A(3;6) có thuộc đồ thị hàm số y = ax^2 hay không, ta thay vào tọa độ của điểm A vào phương trình y = ax^2 với a = 1/4. Ta được 6 = (1/4)*3^2 không xác định, do đó điểm A không thuộc đồ thị hàm số trên.
a) Để tìm hệ số a, ta thay vào tọa độ của điểm M vào phương trình y = ax^2. Ta được 1 = a*2^2 => a = 1/4.