Bài tập 6 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một con thuyền đang neo ở một điểm...
Câu hỏi:
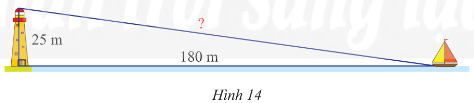
Bài tập 6 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m. Cho biết tháp hải đăng cao 25 m. Hãy tính khoảng cách từ thuyền đến ngọn hải đăng
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Đạt
Để giải bài toán này, chúng ta có thể áp dụng định lí Pythagore. Gọi khoảng cách từ thuyền đến ngọn hải đăng là x, chân tháp hải đăng đến ngọn hải đăng là 25 m, khoảng cách từ thuyền đến chân tháp hải đăng là 180 m.
Ta có:
$(180)^{2} + (25)^{2} = x^{2}$
$32400 + 625 = x^{2}$
$33025 = x^{2}$
$x \approx \sqrt{33025}$
$x \approx 181.73$ m
Vậy, khoảng cách từ thuyền đến ngọn hải đăng là khoảng 181.73 m.
Ta có:
$(180)^{2} + (25)^{2} = x^{2}$
$32400 + 625 = x^{2}$
$33025 = x^{2}$
$x \approx \sqrt{33025}$
$x \approx 181.73$ m
Vậy, khoảng cách từ thuyền đến ngọn hải đăng là khoảng 181.73 m.
Câu hỏi liên quan:
- 1. Định lí PythagoreThực hành 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tính độ...
- Vận dụng 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một chiếc ti vi màn hình phẳng có...
- 2. Định lí Pythagore đảoThực hành 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm tam...
- Vận dụng 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Nam dự định làm một cái eke...
- 3. Vận dụng định lí PythagoreThực hành 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính...
- Vận dụng 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính ciều dài cần cẩu AB trong Hình...
- Bài tậpBài tập 1 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC vuông tại...
- Bài tập 2 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ cao của con diều so với mặt...
- Bài tập 3 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Lần lượt tính độ dài các cạnh huyền...
- Bài tập 4 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Chứng minh rằng tam giác ABC vuông...
- Bài tập 5 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho biết thang của một xe cứu hỏa có...
- Khởi động trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hãy so sánh diện tích hình...
- Khám phá 1 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho một tam giác vuông có hai...
- Khám phá 2 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Vẽ vào vở tam giác ABC có AB =...






Tính khoảng cách từ thuyền đến ngọn hải đăng bằng căn bậc hai của (180^2 - 25^2) = căn bậc hai của 32125 ≈ 179.18 m sử dụng công thức Pythagoras.
Áp dụng công thức của tam giác vuông, ta có khoảng cách từ thuyền đến ngọn hải đăng là căn bậc hai của 180^2 - 25^2 = căn bậc hai của 32125 ≈ 179.18 m.
Sử dụng định lí Pythagoras, ta xác định khoảng cách từ thuyền đến ngọn hải đăng bằng căn bậc hai của (180^2 - 25^2) = căn bậc hai của 32125 ≈ 179.18 m.
Theo định lý Pythagoras, ta có cạnh huyền bình phương bằng tổng bình phương của hai cạnh vuông góc với nhau. Khoảng cách từ thuyền đến ngọn hải đăng sẽ là căn bậc hai của (180^2 - 25^2) = căn bậc hai của 32125 ≈ 179.18 m.