Bài tập 2 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ cao của con diều so với mặt...
Câu hỏi:
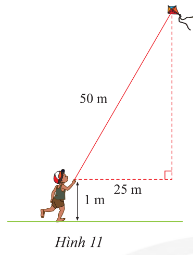
Bài tập 2 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ cao của con diều so với mặt đất (Hình 11).
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
Để giải bài toán này, ta có thể sử dụng định lí Pythagore cho tam giác vuông ABC như sau:Gọi AB là cánh dài, BC là cánh ngang và AC là độ cao của con diều so với mặt đất. Áp dụng định lí Pythagore ta có: $AB^{2}=AC^{2}+BC^{2}$.Từ đó, ta tính được $AC^{2}=AB^{2}-BC^{2}=50^{2}-25^{2}=1875$.Do đó, $AC=25\sqrt{3}$ (m).Vậy, độ cao của con diều so với mặt đất là $25\sqrt{3}+1\approx 44.3$ (m).
Câu hỏi liên quan:
- 1. Định lí PythagoreThực hành 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tính độ...
- Vận dụng 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một chiếc ti vi màn hình phẳng có...
- 2. Định lí Pythagore đảoThực hành 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm tam...
- Vận dụng 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Nam dự định làm một cái eke...
- 3. Vận dụng định lí PythagoreThực hành 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính...
- Vận dụng 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính ciều dài cần cẩu AB trong Hình...
- Bài tậpBài tập 1 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC vuông tại...
- Bài tập 3 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Lần lượt tính độ dài các cạnh huyền...
- Bài tập 4 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Chứng minh rằng tam giác ABC vuông...
- Bài tập 5 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho biết thang của một xe cứu hỏa có...
- Bài tập 6 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một con thuyền đang neo ở một điểm...
- Khởi động trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hãy so sánh diện tích hình...
- Khám phá 1 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho một tam giác vuông có hai...
- Khám phá 2 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Vẽ vào vở tam giác ABC có AB =...






Ngoài ra, để tính độ cao của con diều so với mặt đất, ta cũng có thể sử dụng phương pháp hình học. Vẽ một hình vuông có cạnh bằng bán kính của hình tròn và một tam giác vuông có hai cạnh góc vuông là độ cao của con diều và chiều dài của dây. Từ đó, ta có thể tính được độ cao của con diều.
Một cách khác để giải bài toán này là sử dụng phương pháp thể tích. Ta có thể xem con diều như một cầu nhỏ với bán kính b và tính thể tích của cầu đó. Sau đó, ta sẽ có độ cao của con diều so với mặt đất là căn bậc hai của thể tích đó.
Cách khác, ta cũng có thể xem xét tam giác vuông có hai cạnh góc vuông kéo dài từ con diều đến hai đầu dây và mặt đất. Sử dụng công thức trigonometri sin hoặc cos để tính độ cao của con diều.
Để tính độ cao của con diều so với mặt đất, ta có thể sử dụng định lí Pytago: c^2 = a^2 + b^2. Trong trường hợp này, ta có c là độ cao của con diều, a là chiều dài của dây và b là bán kính của hình tròn. Sau đó, ta có thể giải phương trình để tìm ra độ cao của con diều.