Bài tập 6.34 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho đồ thị ba hàm số...
Câu hỏi:
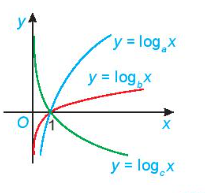
Bài tập 6.34 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho đồ thị ba hàm số $y=\log_{a}x, y=\log_{b}x$ và $y=\log_{c}x$ như hình trên. Mệnh đề nào sau đây là đúng?
A. a>b>c
B. b>a>c
C. a>c>b
D. b>c>a
Câu trả lời:
Người trả lời: GV. Đỗ Văn Việt
Để giải bài toán này, chúng ta có thể áp dụng tính chất của hàm logarit để so sánh các hằng số a, b, c.Phương pháp giải:Ta có hàm số $y=\log_{a}x$ là hàm số tăng khi a > 1, và giảm khi 0 < a < 1.Tương tự, hàm số $y=\log_{b}x$ cũng là hàm số tăng khi b > 1, và giảm khi 0 < b < 1.Cuối cùng, hàm số $y=\log_{c}x$ là hàm số giảm khi c > 1, và tăng khi 0 < c < 1.Với điều kiện trên, ta suy ra a < b vì hàm số logarit với càng cơ số lớn sẽ tăng càng nhanh, và ngược lại với cơ số nhỏ. Tương tự, suy ra b < c.Do đó, mệnh đề đúng sẽ là B. b > a > c.*Câu trả lời chi tiết:*Trong bài toán, chúng ta cần so sánh giữa các hằng số a, b, c trong các hàm số logarit tương ứng.Ta biết rằng hàm số $y=\log_{a}x$ là hàm số tăng khi a > 1, và giảm khi 0 < a < 1.Tương tự, hàm số $y=\log_{b}x$ cũng là hàm số tăng khi b > 1, và giảm khi 0 < b < 1.Cuối cùng, hàm số $y=\log_{c}x$ là hàm số giảm khi c > 1, và tăng khi 0 < c < 1.Do đó, ta có a < b vì hàm số logarit với cơ số lớn sẽ tăng càng nhanh, và ngược lại với cơ số nhỏ. Tương tự, suy ra b < c.Với những suy luận trên, mệnh đề đúng sẽ là B. b > a > c.
Câu hỏi liên quan:
- A - TRẮC NGHIỆMBài tập 6.27 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hai số...
- Bài tập 6.28 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Rút gọn biểu thức...
- Bài tập 6.29 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hai số thực dương a,b...
- Bài tập 6.30 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho bốn số thực dương a,b,x...
- Bài tập 6.31 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Đặt $\log_2(5) = a...
- Bài tập 6.32 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hàm số $y=2^{x}$. Khẳng...
- Bài tập 6.33 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Hàm số nào sau đây đồng...
- B - TỰ LUẬNBài tập 6.35 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho 0 <...
- Bài tập 6.36 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Giải các phương trình...
- Bài tập 6.37 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Tìm tập xác định của các...
- Bài tập 6.38 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Lạm phát là sự tăng mức giá...
- Bài tập 6.39 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Giả sử quá trình nuôi cấy...
- Bài tập 6.40 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Vào năm 1938, nhà vật lí...
Bình luận (0)





