Bài tập 2 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, biết DE // BC...
Câu hỏi:
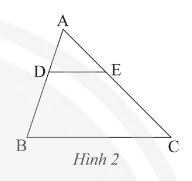
Bài tập 2 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, biết DE // BC (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. $\frac{AD}{DB}=\frac{AE}{EC}$
B. $\frac{AD}{AB}=\frac{AE}{AC}$
C. $\frac{AE}{AC}=\frac{DE}{BC}$
D. $\frac{DB}{AB}=\frac{DE}{BC}$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đức
Để giải bài toán này, ta sẽ sử dụng định lí của Tam giác đồng dạng.Phương pháp giải 1:Gọi I là giao điểm của DE và AC.Ta có $\frac{AD}{DB}=\frac{AI}{IC}$(vì tam giác AID và BIC đồng dạng)$\frac{AE}{EC}=\frac{AI}{IC}$(vì tam giác AIE và CIE đồng dạng)$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$Vậy khẳng định A đúng.Phương pháp giải 2:Gọi K là giao điểm của DE và AB.Ta có $\frac{AD}{AB}=\frac{AK}{KB}$(vì tam giác AKD và BKB đồng dạng)$\frac{AE}{AC}=\frac{AK}{KC}$(vì tam giác AKE và CKC đồng dạng)$\Rightarrow \frac{AD}{AB}=\frac{AE}{AC}$Vậy khẳng định B đúng.Phương pháp giải 3:Để chứng minh khẳng định C đúng, ta cần chứng minh tam giác ADE đồng dạng với tam giác ACB.Gọi H là giao điểm của DE và AB.Ta có $\widehat{ADE}=\widehat{ACB}$(cùng nội tiếp trong hình)$\widehat{DAE}=\widehat{CAB}$(do DE // BC)$\Rightarrow \Delta ADE \sim \Delta ACB$$\Rightarrow \frac{AE}{AC}=\frac{DE}{BC}$Vậy khẳng định C đúng.Vậy khẳng định D sai.Vậy câu trả lời cho câu hỏi là: Khẳng định D sai.
Câu hỏi liên quan:
- Câu hỏi trắc nghiệmChọn phương án đúngBài tập 1 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 3 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 3, biết AM = 3 cm, MN = 4...
- Bài tập 4 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác MNP có MD là tia phân...
- Bài tập 5 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hai đoạn thẳng AB = 12 cm và CD...
- Bài tập 6 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 4, biết MN // BC, AN = 4...
- Bài tập 7 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 5, biết MN // DE, MN = 6 cm...
- Bài tập 8 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, một đường thẳng...
- Bài tập 9 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác biết AM là đường phân...
- Bài tập tự luậnBài tập 10 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC và...
- Bài tập 11 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Độ cao AN và chiều dài bóng...
- Bài tập 12 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có BC bằng 30 cm....
- Bài tập 13 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 8
- Bài tập 14 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 9
- Bài tập 15 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tứ giác ABCD có AC và BD cắt...
- Bài tập 16 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình bình hành ABCD. Đường...
- Bài tập 17 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Quan sát Hình 11, chứng...






Vậy, trong các khẳng định trên, khẳng định C là sai, các khẳng định còn lại là đúng.
Khẳng định D đúng vì theo định lí tỉ lệ cùng chiều ta có $ rac{DB}{AB}= rac{DE}{BC}$
Khẳng định C sai vì DE//BC nên không thể bằng nhau $ rac{AE}{AC}= rac{DE}{BC}$
Khẳng định B đúng vì theo định lí tỉ lệ cùng chiều ta có $ rac{AD}{AB}= rac{AE}{AC}$
Khẳng định A sai vì theo định lí Thales ta có AB//DE nên $ rac{AD}{DB}= rac{AE}{EC}$