Bài tập 13 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 8

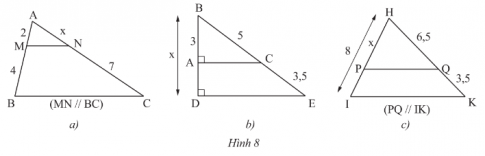
Phương pháp giải:

a) Xét tam giác ABC có MN // BC, theo định lí Thales ta có: $\frac{AM}{MB}=\frac{AN}{NC}$.
Suy ra $\frac{2}{4}=\frac{x}{7}$.
Vậy $x = \frac{7}{2}$.

b) Gọi $E$ là giao điểm của $DE$ và $AC$. Ta có $CA\perp BD$ và $DE\perp BD$, nên $AC \parallel DE$.
Suy ra $\frac{AB}{BD}=\frac{BC}{BE}$.
Từ đó, $\frac{3}{x}=\frac{5}{5+3,5}$.
Vậy $x = 5,1$.

c) Xét tam giác HIK có PQ // IK. Ta có $\frac{HP}{HI}=\frac{HQ}{HK}$.
Suy ra $\frac{x}{8}=\frac{6,5}{6,5+3,5}$.
Vậy $x = 5,2$.

Vậy độ dài $x$ trong Hình 8 là:
a) $x = \frac{7}{2}$
b) $x = 5,1$
c) $x = 5,2$