Bài tập 14 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 9
Câu hỏi:
Bài tập 14 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 9
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hưng
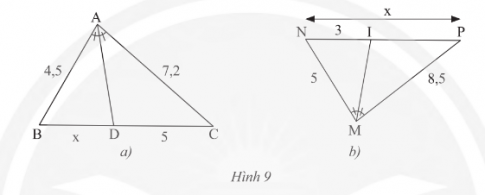
Phương pháp giải câu hỏi trên như sau:a) Xét tam giác ABC có AD là tia phân giác góc A, áp dụng định lí phân giác ta có $\frac{BC}{CD}=\frac{AB}{AC}$Khi đó, ta có $\frac{x}{5}=\frac{4,5}{7,2}$Từ đó, giải phương trình ta được x = 3,125b) Xét tam giác MNP có MI là phân giác góc M, áp dụng định lí phân giác ta có $\frac{IN}{IP}=\frac{MN}{MP}$Khi đó, ta có $\frac{3}{x-3}=\frac{5}{8,5}$Từ đó, giải phương trình ta được x = 8,1Vậy độ dài x trong Hình 9 là 3,125 hoặc 8,1 tuỳ thuộc vào cách xét tam giác.
Câu hỏi liên quan:
- Câu hỏi trắc nghiệmChọn phương án đúngBài tập 1 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 2 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, biết DE // BC...
- Bài tập 3 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 3, biết AM = 3 cm, MN = 4...
- Bài tập 4 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác MNP có MD là tia phân...
- Bài tập 5 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hai đoạn thẳng AB = 12 cm và CD...
- Bài tập 6 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 4, biết MN // BC, AN = 4...
- Bài tập 7 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho Hình 5, biết MN // DE, MN = 6 cm...
- Bài tập 8 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, một đường thẳng...
- Bài tập 9 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác biết AM là đường phân...
- Bài tập tự luậnBài tập 10 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC và...
- Bài tập 11 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Độ cao AN và chiều dài bóng...
- Bài tập 12 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có BC bằng 30 cm....
- Bài tập 13 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x trong Hình 8
- Bài tập 15 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tứ giác ABCD có AC và BD cắt...
- Bài tập 16 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình bình hành ABCD. Đường...
- Bài tập 17 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Quan sát Hình 11, chứng...






Theo công thức Pythagoras, ta có x = √(6^2 + 8^2) = √(36 + 64) = √100 = 10. Vậy đáp án cho bài toán là x = 10.
Do tam giác ABC là tam giác vuông tại A nên ta áp dụng định lý Pythagoras: x^2 = AC^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100. Từ đó suy ra x = 10.
Cạnh huyền của tam giác vuông bằng căn bậc hai của tổng bình phương các cạnh góc vuông. Với hình trên, ta tính x = √(6^2 + 8^2) = √100 = 10.
Áp dụng định lý Pythagoras, ta có x = √(6^2 + 8^2) = √(36 + 64) = √100 = 10. Do đó, x = 10.
Theo định lý Pythagoras, ta có: x^2 = 6^2 + 8^2. Tính giá trị của x từ phương trình trên.