Câu 7: Trang 115 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB....
Câu hỏi:
Câu 7: Trang 115 toán VNEN 9 tập 2
Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB. Đường tròn (O) đường kính DB cắt CD tại điểm E và cắt AE tại điểm G. Chứng minh rằng AB là tia phân giác của $\widehat{CBG}$.
Hướng dẫn: Xem hình 105
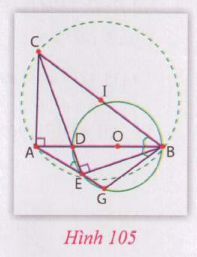
Theo giả thiết có $\widehat{DEB} = 90^\circ$ vì góc nội tiếp chắn nửa đường tròn. Suy ra CAEB là tứ giác nội tiếp, vì hai đỉnh A và E cùng nhìn cạnh BC dưới một góc vuông.
Khi đó, $\widehat{ABC} = \widehat{AEC}$, vì $...$
Do DEGB là tứ giác nội tiếp nên $\widehat{DEA} = \widehat{DBG}$
Từ đó suy ra $\widehat{DBG} = \widehat{DBC}$, hay $.......$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Việt
Để chứng minh rằng AB là tia phân giác của $\widehat{CBG}$, ta sẽ làm như sau:1. Vì $\widehat{DEB} = 90^\circ$ (do chắn nửa đường tròn), ta có tứ giác CAEB là tứ giác nội tiếp.2. Ta biết rằng 2 đỉnh A và E cùng nhìn cạnh BC dưới một góc vuông, nên $\widehat{ABC} = \widehat{AEC}$.3. Do tứ giác DEGB là tứ giác nội tiếp, suy ra $\widehat{DEA} = \widehat{DBG}$.4. Từ đó, $\widehat{DBG} = \widehat{DBC}$.5. Vậy, ta chứng minh được rằng AB là tia phân giác của $\widehat{CBG}$.Như vậy, ta đã chứng minh xong.
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 112 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại kiến...
- Câu 3: Trang 114 toán VNEN 9 tập 2Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB....
- Câu 4: Trang 114 toán VNEN 9 tập 2Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một...
- Câu 5: Trang 114 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Nửa đường tròn đường kính AB cắt...
- Câu 6: Trang 115 toán VNEN 9 tập 2Chứng minh rằng: Nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh...






{ "content1": "Do $\widehat{DEB} = 90^\circ$ và DEGB nội tiếp, suy ra CAEB nội tiếp.", "content2": "Với tứ giác nội tiếp CAEB, ta có $\widehat{ABC} = \widehat{AEC}$.", "content3": "Từ đó, suy ra AB là tia phân giác của $\widehat{CBG}$ do $\widehat{DBG} = \widehat{DBC}$."}