Câu 3: Trang 114 toán VNEN 9 tập 2Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB....
Câu 3: Trang 114 toán VNEN 9 tập 2
Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB. Lấy AC làm cạnh, vẽ tam giác đều ACD sao cho D và B là hai điểm khác phía so với đường thẳng AC. Gọi E là giao điểm của CD với cung AB. Gọi M là trung điểm của đoạn thẳng DC. Chứng minh rằng: Khi điểm C di động trên cung AB thì điểm M thuộc nửa đường tròn đường kính AE.
Hướng dẫn: Xem hình 101
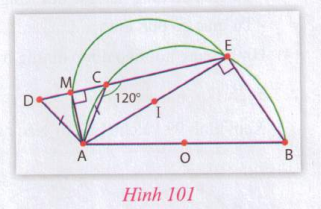
Theo giả thiết ta có $\widehat{ACD} = 60^\circ$ nên $\widehat{ACE} = 120^\circ$ mà ACEB là tứ giác nội tiếp nên $\widehat{ABE} = 60^\circ$.
Do A, B cố định, $\widehat{ABE} = 60^\circ$ (không đổi) nên điểm E cố định.
Theo giả thiết ACD là tam giác đều và M là trung điểm của đoạn DC nên $\widehat{AMC} = 90^\circ$, hay $\widehat{90^\circ}$.
Như vậy, do điểm M di động nhưng luôn nhìn đoạn thẳng AE $...........$
- C. Hoạt động luyện tậpCâu 1: Trang 112 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại kiến...
- Câu 4: Trang 114 toán VNEN 9 tập 2Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một...
- Câu 5: Trang 114 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Nửa đường tròn đường kính AB cắt...
- Câu 6: Trang 115 toán VNEN 9 tập 2Chứng minh rằng: Nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh...
- Câu 7: Trang 115 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB....






{ "content1": "Do $\angle{ACD} = 60^\circ$, ta có $\angle{ACE} = 120^\circ$. Vì tứ giác ACEB nội tiếp nên $\angle{ABE} = 60^\circ$.", "content2": "Với $AC = AE$, ta có $\angle{ACE} = \angle{AEC} = 60^\circ$. Khi $C$ di chuyển trên cung $AB$, $\angle{ACE}$ không đổi nên $E$ là điểm cố định.", "content3": "Vì $\angle{AMC} = 90^\circ$ ($M$ là trung điểm của $CD$), nên $M$ luôn nằm trên nửa đường tròn đường kính $AE$ khi $C$ di chuyển trên cung $AB$."}