Câu 4: Trang 114 toán VNEN 9 tập 2Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một...
Câu hỏi:
Câu 4: Trang 114 toán VNEN 9 tập 2
Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. Ngược lại, tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó là tứ giác nội tiếp.
Hướng dẫn: Xem hình 102
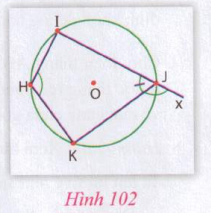
Nếu HIJK là tứ giác nội tiếp thì $\widehat{IHK} + \widehat{IJK} = 180^\circ$.
Mặt khác, $\widehat{IJK}$ và $\widehat{KJx}$ là hai góc kề bù, nên $\widehat{IJK} + \widehat{KJx} = 180^\circ$. Từ đó suy ra $....$
Ngược lại, nếu $\widehat{IHK} = \widehat{KJx}$ thì $\widehat{IHK} + \widehat{IJK} = \widehat{IJK} + \widehat{KJx} = 180^\circ$
Từ đó suy ra HIJK $.........$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Dung
Để chứng minh rằng trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó, ta làm như sau:Gọi tứ giác nội tiếp là HIJK. Theo tính chất của tứ giác nội tiếp, ta có: $\widehat{IHK} + \widehat{IJK} = 180^\circ$.Xét hai góc kề bù $\widehat{IJK}$ và $\widehat{KJx}$, ta có $\widehat{IJK} + \widehat{KJx} = 180^\circ$.Từ đó suy ra: $\widehat{IJK} = \widehat{KJx}$.Ngược lại, nếu $\widehat{IHK} = \widehat{KJx}$, suy ra $\widehat{IHK} + \widehat{IJK} = \widehat{IJK} + \widehat{KJx} = 180^\circ$.Từ đó, HIJK là tứ giác nội tiếp.Vậy, ta đã chứng minh được rằng trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó, và ngược lại.
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 112 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại kiến...
- Câu 3: Trang 114 toán VNEN 9 tập 2Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB....
- Câu 5: Trang 114 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Nửa đường tròn đường kính AB cắt...
- Câu 6: Trang 115 toán VNEN 9 tập 2Chứng minh rằng: Nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh...
- Câu 7: Trang 115 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB....






Vậy nên, ta đã chứng minh được rằng trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó và ngược lại.
Ngược lại, nếu góc IJK = góc KJx, ta có góc IHK + góc IJK = góc IJK + góc KJx = 180 độ, từ đó suy ra tứ giác HIJK là tứ giác nội tiếp.
Nếu tứ giác HIJK là tứ giác nội tiếp thì góc IJK + góc IHK = 180 độ, do đó góc IJK = góc KJx.
Để chứng minh rằng trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó, ta sử dụng tính chất của tứ giác nội tiếp là tổng hai góc trong bằng 180 độ.