Câu 6: Trang 115 toán VNEN 9 tập 2Chứng minh rằng: Nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh...
Câu hỏi:
Câu 6: Trang 115 toán VNEN 9 tập 2
Chứng minh rằng: Nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc $\alpha \;(0 < \alpha < 180^\circ)$ thì đó là tứ giác nội tiếp. Ngược lại, trong một tứ giác nội tiếp, hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc.
Hướng dẫn: Xem hình 104
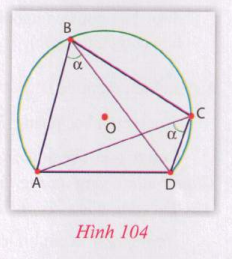
Giả sử tứ giác ABCD có hai đỉnh B và C cùng nhìn cạnh AD dưới cùng một góc $\alpha \;(0 < \alpha < 180^\circ)$.
Khi đó, B và C cùng thuộc cung chứa góc $\alpha $ (tâm O) dựng trên cạnh AD.
Tức là bốn điểm A, B, C, D cùng thuộc đường tròn (O), suy ra $.....$
Ngược lại, nếu ABCD là tứ giác nội tiếp thì $\widehat{ABD} = \widehat{ACD}$ vì $.............$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Long
Để chứng minh rằng tứ giác ABCD là tứ giác nội tiếp khi hai đỉnh B và C cùng nhìn cạnh AD dưới cùng một góc $\alpha$, ta có thể áp dụng định lí góc nội tiếp trong đường tròn. Giả sử B và C cùng thuộc cung chứa góc $\alpha$ (tâm O) dựng trên cạnh AD. Khi đó, tứ giác ABCD cùng thuộc đường tròn (O), do đó ABCD là tứ giác nội tiếp.Ngược lại, nếu ABCD là tứ giác nội tiếp, ta có $\widehat{ABD} = \widehat{ACD}$ vì hai góc này đều chắn cùng một cung AD trên đường tròn. Do đó, hai đỉnh kề nhau trong tứ giác nội tiếp cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc. Vậy ta đã chứng minh được cả hai phần của câu hỏi. Do đó, ta có câu trả lời đầy đủ và chi tiết: "Để chứng minh rằng tứ giác ABCD là tứ giác nội tiếp khi hai đỉnh B và C cùng nhìn cạnh AD dưới cùng một góc $\alpha$, ta áp dụng định lí góc nội tiếp trong đường tròn. Giả sử B và C cùng thuộc cung chứa góc $\alpha$ (tâm O) dựng trên cạnh AD. Khi đó, tứ giác ABCD cùng thuộc đường tròn (O), do đó ABCD là tứ giác nội tiếp. Ngược lại, nếu ABCD là tứ giác nội tiếp, ta có $\widehat{ABD} = \widehat{ACD}$ vì hai góc này đều chắn cùng một cung AD trên đường tròn. Do đó, hai đỉnh kề nhau trong tứ giác nội tiếp cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc. Vậy ta đã chứng minh được cả hai phần của câu hỏi."
Câu hỏi liên quan:
- C. Hoạt động luyện tậpCâu 1: Trang 112 toán VNEN 9 tập 2Thực hiện các hoạt động sau để ôn lại kiến...
- Câu 3: Trang 114 toán VNEN 9 tập 2Cho nửa đường tròn đường kính AB và điểm C di động trên cung AB....
- Câu 4: Trang 114 toán VNEN 9 tập 2Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một...
- Câu 5: Trang 114 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Nửa đường tròn đường kính AB cắt...
- Câu 7: Trang 115 toán VNEN 9 tập 2Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB....






Như vậy, từ các tính chất trên, chúng ta chứng minh được mệnh đề ban đầu.
Trong tứ giác nội tiếp, hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc vì cả hai góc bằng nhau.
Do đó, nếu tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α, thì đó là tứ giác nội tiếp.
Ngược lại, nếu ABCD là tứ giác nội tiếp thì góc ABD bằng góc ACD vì cả hai góc đều chứa cùng một cung tròn.
Tức là bốn điểm A, B, C, D cùng thuộc đường tròn (O), do đó tứ giác ABCD là tứ giác nội tiếp.