Câu 4: Trang 64 sách VNEN 9 tập 1Cho tam giác ABC vuông tại A có BC = 10cm,$\frac{AB}{AC}$...
Câu hỏi:
Câu 4: Trang 64 sách VNEN 9 tập 1
Cho tam giác ABC vuông tại A có BC = 10cm, $\frac{AB}{AC}$ = $\frac{3}{4}$
a) Tính độ dài các cạnh AB, AC.
b) Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính độ dài đoạn thẳng MN, MC
Hướng dẫn (h.28)
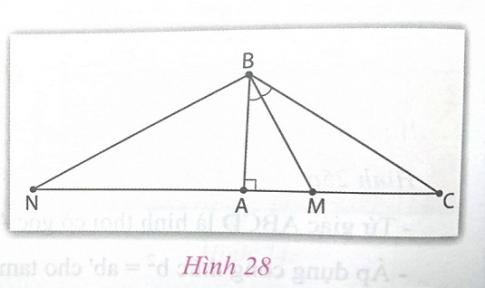
b) + Sử dụng tính chất đường phân giác $\frac{AM}{BA}$ = $\frac{MC}{BC}$ để tính MA, MC.
+ Chú ý rằng hai đường phân giác trong và ngoài của một góc thì vuông góc với nhau. Do đó BM $\perp $ BN. Áp dụng công thức $h^{2}$ = b'.c' cho tam giác vuông BMN thì $AB^{2}$ = AM.AN
Câu trả lời:
Người trả lời: GV. Đỗ Thị Giang
a) Cách làm:- Theo đề bài, ta có: $\frac{AB}{AC}$ = $\frac{3}{4}$.- Áp dụng định lý Pythagoras vào tam giác vuông ABC, ta có: $AB^{2}$ + $AC^{2}$ = $BC^{2}$.- Thay $AB = \frac{3}{4}AC$ vào phương trình trên, ta suy ra AC = 8cm và AB = 6cm.b) Cách làm:- Áp dụng tính chất đường phân giác trong, ta có: $\frac{AM}{BA}$ = $\frac{MC}{BC}$ = $\frac{AC}{BA + BC}$ = $\frac{8}{6 + 10}$ = $\frac{1}{2}$. Từ đó, ta tính được AM = 3cm và MC = 5cm.- Vì hai đường phân giác trong và ngoài của một góc thì vuông góc với nhau, nên BM $\perp$ BN.- Áp dụng công thức $h^{2}$ = b'.c' cho tam giác vuông BMN, ta có: $AB^{2}$ = AM.AN. Từ đó, suy ra MN = AN + AM = 12 + 3 = 15cm.Vậy kết quả là MC = 5cm, MN = 15cm.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 63 sách VNEN 9 tập 1Tính x, y trong mỗi hình sau:
- Câu 2: Trang 64 sách VNEN 9 tập 1Cho tam giác vuông với các cạnh góc vuông có độ dài là 3cm và 4cm....
- Câu 3: Trang 64 sách VNEN 9 tập 1Cho tam giác ABC vuông tại A, phân giác AD. Biết BD =...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 1: Trang 65 sách VNEN 9 tập 1Bài toán lớp 1: Hai vệ...
- Câu 2: Trang 65 sách VNEN 9 tập 1Bài toán lớp 2:Một chiếc băng tải di động có hình dạng như...






Vậy độ dài các cạnh và đoạn thẳng trong tam giác ABC là AB = 6cm, AC = 8cm, MN = 4cm và MC = 4.8cm.
b) MN = 4cm, MC = 4.8cm
a) AB = 6cm, AC = 8cm