Câu 2: Trang 100 sách VNEN 9 tập 1Cho đường tròn (O) và một điểm E nằm ngoài đường tròn, vẽ đường...
Câu hỏi:
Câu 2: Trang 100 sách VNEN 9 tập 1
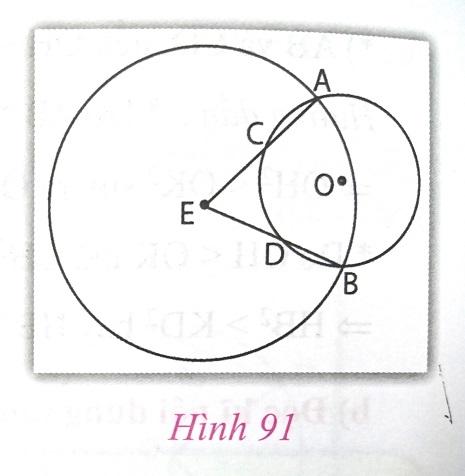
Cho đường tròn (O) và một điểm E nằm ngoài đường tròn, vẽ đường tròn (E) cắt đường tròn (O) tại hai điểm A và B (h.91). Các đoạn thẳng EA và EB lần lượt cắt đường tròn (O) tại C và D (cho như hình vẽ). Chứng minh rằng hai dây AC và BD của đường tròn (O) bằng nhau.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Hạnh
Để chứng minh rằng hai dây AC và BD của đường tròn (O) bằng nhau, ta có thể sử dụng một số phương pháp sau:Cách 1: Sử dụng tính chất của tứ giác tứ giác nội tiếp.- Ta có tứ giác OACD và tứ giác OBDC nội tiếp.- Do đó, tứ giác OACD và tứ giác OBDC là tứ giác nội tiếp cùng chứa đường chéo AC và BD.- Từ đó, ta suy ra AC = BD.Cách 2: Sử dụng tính chất của các tam giác đồng dạng.- Ta thấy các tam giác OAE và OBE đồng dạng (c.c.c).- Do đó, ta có $\frac{EA}{EB} = \frac{OA}{OB} = 1$ (vì OA = OB).- Suy ra EA = EB.- Tương tự, ta có $\frac{AC}{BD} = \frac{EA}{EB} = 1$.- Từ đó, suy ra AC = BD.Vậy, ta đã chứng minh được rằng hai dây AC và BD của đường tròn (O) bằng nhau.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 99 sách VNEN 9 tập 1Cho đường tròn tâm O, bán kính 13cm, dây AB...
- Câu 3: Trang 100 sách VNEN 9 tập 1Cho đường tròn (O) bán kính 2,5cm, dây AB = 4cm. Vẽ dây CD song...
- Câu 4: Trang 100 sách VNEN 9 tập 1Cho hình 92, trong đó hai đường tròn cùng có tâm O. Cho biết AB...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 1: Trang 100 sách VNEN 9 tập 1Cho đường tròn (O),...
- Câu 2: Trang 100 sách VNEN 9 tập 1Đố: Nhà ba bạn An, Cường, Thái ở ba địa điểm như hình 94. Hỏi...
- Câu 3: Trang 101 sách VNEN 9 tập 1Cho hình 95. Trên đường tròn (O) lấy hai dây AM và BN bằng nhau...






Như vậy, ta đã chứng minh được hai dây AC và BD của đường tròn (O) bằng nhau. Điều cần chứng minh.
Từ đó suy ra AM/MB = CM/MD. Với AM = CM (vì A và C là hai điểm cắt của đường tròn (E) với đường tròn (O), cùng với đúng một dây cung thì các dây cung tương ứng bằng nhau), ta suy ra MB = MD.
Gọi M là giao điểm của AC và BD, ta có AMB và CMD là hai tam giác cùng chứa một góc nên theo nguyên lý cùng chứa góc thì tỉ lệ độ dài các cạnh bằng nhau.
Để chứng minh hai dây AC và BD của đường tròn (O) bằng nhau, ta sẽ sử dụng tính chất của dây cung và dây tiếp tuyến.