C. Hoạt động luyện tậpCâu 1: Trang 89 toán VNEN 9 tập 2Xem hình 45, biết $\widehat{ABC} = 3...
Câu hỏi:
C. Hoạt động luyện tập
Câu 1: Trang 89 toán VNEN 9 tập 2
Xem hình 45, biết $\widehat{ABC} = 30^\circ$
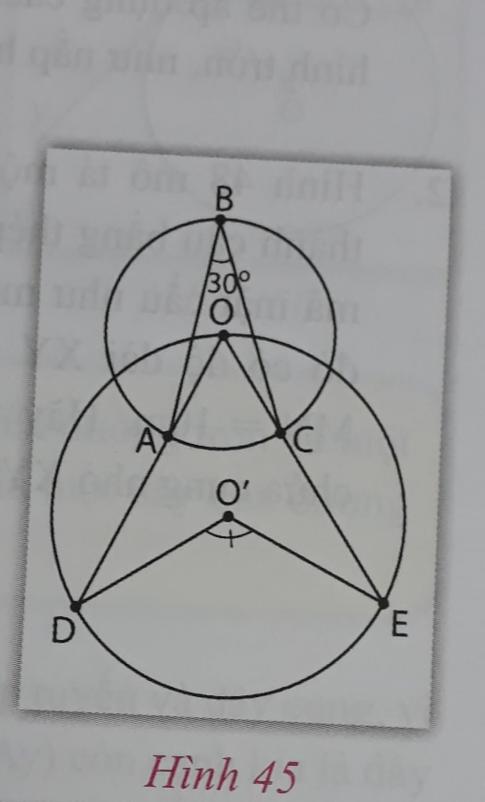
a) Với đường tròn (O), số đo của góc $\widehat{AOC}$ bằng bao nhiêu? Vì sao?
b) Với đường tròn (O'), số đo của $\widehat{DO'E}$ bằng bao nhiêu? Vì sao?
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
Để giải bài toán trên, ta cần sử dụng tính chất của các góc nội tiếp và góc ngoại tiếp trên đường tròn.
Cách làm:
a) Với đường tròn (O):
- Ta có $\widehat{AOC}$ là góc ngoại tiếp của $\widehat{ABC}$ nằm trên cùng một dây tròn AB với góc $\widehat{ABC}$, nên $\widehat{AOC} = 2\widehat{ABC}$.
- Từ đó, $\widehat{AOC} = 2 \times 30^\circ = 60^\circ$.
b) Với đường tròn (O'):
- Góc $\widehat{DO'E}$ cũng là góc ngoại tiếp của góc $\widehat{AOC}$, nên $\widehat{DO'E} = 2\widehat{AOC}$.
- Từ đó, $\widehat{DO'E} = 2 \times 60^\circ = 120^\circ$.
Vậy,
a) Với đường tròn (O), $\widehat{AOC} = 60^\circ$.
b) Với đường tròn (O'), $\widehat{DO'E} = 120^\circ$.
Cách làm:
a) Với đường tròn (O):
- Ta có $\widehat{AOC}$ là góc ngoại tiếp của $\widehat{ABC}$ nằm trên cùng một dây tròn AB với góc $\widehat{ABC}$, nên $\widehat{AOC} = 2\widehat{ABC}$.
- Từ đó, $\widehat{AOC} = 2 \times 30^\circ = 60^\circ$.
b) Với đường tròn (O'):
- Góc $\widehat{DO'E}$ cũng là góc ngoại tiếp của góc $\widehat{AOC}$, nên $\widehat{DO'E} = 2\widehat{AOC}$.
- Từ đó, $\widehat{DO'E} = 2 \times 60^\circ = 120^\circ$.
Vậy,
a) Với đường tròn (O), $\widehat{AOC} = 60^\circ$.
b) Với đường tròn (O'), $\widehat{DO'E} = 120^\circ$.
Câu hỏi liên quan:
- Câu 2: Trang 89 toán VNEN 9 tập 2Xem hình 46, các điểm A, B, C thuộc đường tròn có PQ là dây...
- Câu 3: Trang 89 toán VNEN 9 tập 2Cho hai đường tròn có tâm lần lượt là E và F cắt nhau tại hai điểm...
- Câu 4: Trang 89 toán VNEN 9 tập 2Hai đường tròn bằng nhau có tâm tương ứng là I và J cắt nhau tại...
- D. E Hoạt động vận dụng và tìm tòi, mở rộngCâu 1: Trang 90 toán VNEN 9 tập 2Bạn Hoàng đã vẽ một...
- Câu 2: Trang 90 toán VNEN 9 tập 2Hình 48 mô tả một chiếc cầu bắc qua sông, có thành cầu bằng thép...






f) Bằng cách sử dụng tính chất của góc lưỡng phương và góc nửa đường tròn, ta có thể xác định được góc AOC và góc DO'E trong bài toán trên.
e) Góc AOC và góc DO'E là các góc lưỡng phương, nghĩa là chúng có cùng một đỉnh và hai cạnh cạnh nhau, nhưng không phải hai cạnh cùng phía.
d) Để tính góc AOC và DO'E, ta cũng có thể sử dụng tính chất của góc nửa đường tròn, là 180 độ.
c) Góc ở tâm (AOC) và góc ở tâm (DO'E) đều bằng góc nửa đường tròn tương ứng, khi chúng đều có mở rộng qua tâm.
b) Với đường tròn (O'), số đo của góc DO'E là 60 độ. Ta có thể suy luận được bằng cách sử dụng tính chất góc ở tâm.