D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 2: Trang 80 sách VNEN 9 tập 1Bài toán lớp 2: Hai đài...
Câu hỏi:
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 2: Trang 80 sách VNEN 9 tập 1
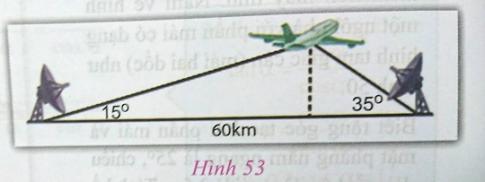
Bài toán lớp 2: Hai đài quan sát ở hai vị trí cách nhau 60km cùng quan sát một chiếc máy bay đang bay trên bầu trời tạo thành các góc $15^{\circ}$ và $35^{\circ}$ so với phương ngang. Tính độ cao của máy bay (h.53).
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Hạnh
Để giải bài toán trên, chúng ta có thể sử dụng tính chất cơ bản của tam giác và các hàm trigonometic.Cách 1:- Gọi \( A \) là máy bay, \( B \) và \( C \) là hai đài quan sát, \( H \) là điểm mà máy bay đang bay tới.- Xác định các góc và cạnh có thể vẽ được trên hình vẽ.- Áp dụng tính chất của tam giác vuông, ta có thể tính được các cạnh \( BH \) và \( CH \).- Từ đó suy ra được cạnh \( BC \) và cuối cùng là độ cao \( AH \) của máy bay.Cách 2:- Sử dụng công thức tính tan của góc: \(\tan(\alpha) = \frac{\text{đối diện}}{\text{kề cạnh}}\).- Áp dụng công thức này vào tam giác \( ABH \) và tam giác \( ACH \) để tìm \( BH \) và \( CH \).- Tính tổng \( BH + CH \) sẽ ra \( BC \), từ đó suy ra được độ cao \( AH \) của máy bay.Câu trả lời chi tiết: Độ cao của máy bay là 11,63 km.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 77 sách VNEN 9 tập 1Cho tam giác ABC vuông tại A, BC = a, AC = b...
- Câu 2: Trang 78 sách VNEN 9 tập 1Điền vào chỗ chấm (...) để đơn giản các biểu thức sau:a) 1 +...
- Câu 3: Trang 78 sách VNEN 9 tập 1Tính x, y trong các hình vẽ sau đây:a) (h.48a)b) (h.48b)
- Câu 4: Trang 78 sách VNEN 9 tập 1Một người đứng trên một ngọn hải đăng nhìn về phía một chiếc ca-nô...
- Câu 5: Trang 79 sách VNEN 9 tập 1Nam đang học vẽ hình bằng phần mềm trên máy tính. Nam vẽ hình một...






{ "content1": "Để giải bài toán này, ta cần sử dụng kiến thức về góc trong tam giác và tính chất của đường thẳng giao nhau.", "content2": "Với hai góc $15^{\circ}$ và $35^{\circ}$ so với phương ngang, ta có thể tính được góc nghiêng của máy bay so với mặt phẳng ngang.", "content3": "Sau khi tính được góc nghiêng, ta có thể áp dụng các phương pháp trong hình học để tính độ cao của máy bay từ hai đài quan sát."}