Câu 4: Trang 78 sách VNEN 9 tập 1Một người đứng trên một ngọn hải đăng nhìn về phía một chiếc ca-nô...
Câu hỏi:
Câu 4: Trang 78 sách VNEN 9 tập 1
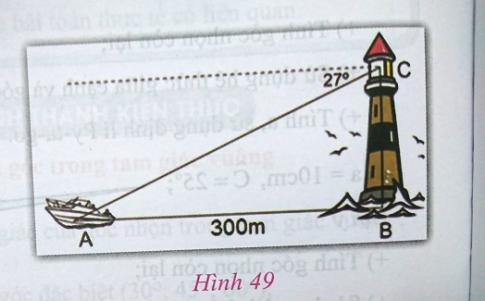
Một người đứng trên một ngọn hải đăng nhìn về phía một chiếc ca-nô trên biển tạo thành một góc $27^{\circ}$ so với phương nằm ngang. Biết ca-nô cách ngọn hải đăng khoảng 300m. Ước lượng chiều cao của ngọn hải đăng
Câu trả lời:
Người trả lời: GV. Đỗ Thị Việt
Cách 1: Để ước lượng chiều cao của ngọn hải đăng, ta thực hiện các bước sau:- Gọi B là ngọn hải đăng, A là vị trí mà người đứng, C là vị trí của chiếc ca-nô.- Kẻ đường thẳng AB và kẻ đường thẳng từ C vuông góc với AB tại D.- Gọi AD = x (đơn vị mét), BC = 300m.- Tính góc BAD, ta có $\angle$BAD = 180$^{\circ}$ - 27$^{\circ}$ = 153$^{\circ}$.- Do BA $\perp$ CD nên tam giác BAD vuông tại A.- Áp dụng công thức tan$\angle$A = $\frac{BC}{AB}$, ta có tan153$^{\circ}$ = $\frac{300}{x}$, từ đó tính được x, có x = $\frac{300}{tan153^{\circ}} \approx 152,9$mVậy chiều cao của ngọn hải đăng là x ≈ 152,9m.Cách 2:- Gọi chiều cao của ngọn hải đăng cần tìm là x (đơn vị mét).- Do góc $\angle$ABD = 27$^{\circ}$ và BC = 300m, ta có $tan27^{\circ} = \frac{x}{300}$.- Từ đó, suy ra x = 300tan27$^{\circ}$ ≈ 152,9m.Vậy chiều cao của ngọn hải đăng là x ≈ 152,9m.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 77 sách VNEN 9 tập 1Cho tam giác ABC vuông tại A, BC = a, AC = b...
- Câu 2: Trang 78 sách VNEN 9 tập 1Điền vào chỗ chấm (...) để đơn giản các biểu thức sau:a) 1 +...
- Câu 3: Trang 78 sách VNEN 9 tập 1Tính x, y trong các hình vẽ sau đây:a) (h.48a)b) (h.48b)
- Câu 5: Trang 79 sách VNEN 9 tập 1Nam đang học vẽ hình bằng phần mềm trên máy tính. Nam vẽ hình một...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 2: Trang 80 sách VNEN 9 tập 1Bài toán lớp 2: Hai đài...
Bình luận (0)





