Bài 5 : Tính khoảng cách AB giữa hai nóc toà cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ...
Câu hỏi:
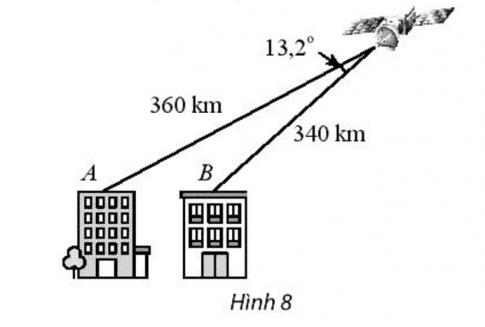
Bài 5 : Tính khoảng cách AB giữa hai nóc toà cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 360 km, 340 km và góc nhìn từ vệ tinh đến A và B là 13,2 độ (Hình 8).
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Giang
Để giải bài toán này, chúng ta có thể áp dụng công thức cosine trong tam giác để tính khoảng cách AB giữa hai nóc toà cao ốc.
Công thức cosine trong tam giác:
\(AB^2 = OA^2 + OB^2 - 2 \cdot OA \cdot OB \cdot \cos{\angle AOB}\)
Lần lượt điền các giá trị đã biết vào công thức:
\(AB^2 = 360^2 + 340^2 - 2 \cdot 360 \cdot 340 \cdot \cos{13.2^\circ}\)
Tính toán:
\(AB^2 \approx 6867.88\)
Kết quả:
\(AB \approx \sqrt{6867.88} \approx 82.87\) km
Vậy, khoảng cách giữa hai nóc toà cao ốc khoảng 83 km.
Công thức cosine trong tam giác:
\(AB^2 = OA^2 + OB^2 - 2 \cdot OA \cdot OB \cdot \cos{\angle AOB}\)
Lần lượt điền các giá trị đã biết vào công thức:
\(AB^2 = 360^2 + 340^2 - 2 \cdot 360 \cdot 340 \cdot \cos{13.2^\circ}\)
Tính toán:
\(AB^2 \approx 6867.88\)
Kết quả:
\(AB \approx \sqrt{6867.88} \approx 82.87\) km
Vậy, khoảng cách giữa hai nóc toà cao ốc khoảng 83 km.
Câu hỏi liên quan:
- Bài 1 : Cho tam giác ABC với BC = a; AC = b; AB = c và a = b. Chứng minh rằng:c2= 2a2(1...
- Bài 2 : Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:a) góc A = 42 độ, góc B =...
- Bài 3 : Để xác định chiều cao của một toà nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế...
- Bài 4 : Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ...
- Bài 6 : Một chiếc tàu khởi hành từ bến cảng, đi về hướng bắc 15 km, sau đó bẻ lái 20 độ về hướng...
Bình luận (0)





