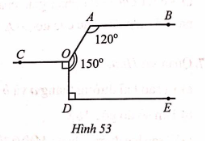
Bài 43: Cho hình 53 có OC và DE cùng vuông góc với OD, $\widehat{BAO}=120^{\circ}...

Cách làm:

1. Vẽ hình và kẻ tia \(OC'\) đối của tia \(OC\).
2. Do \(OC\) và \(DE\) cùng vuông góc với \(OD\), ta có \(\widehat{COD} = \widehat{ODE} = 90^\circ\). Suy ra \(OC \parallel DE\).
3. Ta có \( \widehat{DOC'} + \widehat{ODE} = 180^\circ\) (hai góc trong cùng phía), suy ra \(\widehat{DOC'} = 90^\circ\).
4. Ta có \(\widehat{AOC'} + \widehat{DOC'} = \widehat{AOD}\), suy ra \(\widehat{AOC'} = 60^\circ\).
5. Từ \(\widehat{AOC'}+\widehat{AOC} = 180^\circ\) (hai góc kề bù) suy ra \(\widehat{AOC} = 120^\circ\).
6. Vậy ta có \(\widehat{AOC} = \widehat{OAB}\) và do cùng ở vị trí so le trong, nên \(AB \parallel OC\).
7. Kết hợp với \(OC \parallel DE\), suy ra \(AB \parallel OC \parallel DE\).

Vậy ta đã chứng minh được rằng \(AB \parallel OC \parallel DE\).

Câu trả lời: Chứng minh được rằng AB//OC//DE.