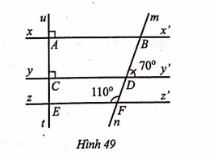
Bài 39: Quan sát hình 49. Chứng tỏ:a) yy'//zz'b) ut $\perp $zz'c) xx' // zz'

a)
Cách 1: Ta có ba góc $\widehat{DFE}, \widehat{DFz'}, \widehat{BDy'}$ tạo thành một tam giác nội tiếp nên tổng của ba góc này bằng 180$^{\circ}$. Vì $\widehat{DFE}=110^{\circ}$ nên $\widehat{DFz'}=180^{\circ}-\widehat{DFE}=180^{\circ}-110^{\circ}=70^{\circ}$. Mà $\widehat{DFz'}=\widehat{BDy'}$ nên yy'//zz'.

Cách 2: Kẻ AD // BC, ta được $\widehat{DFE}=\widehat{CED}$ (cùng chắn hai vòng cung) và $\widehat{CED}=\widehat{DFz'}$ (cùng chắn hai vòng cung) nên $\widehat{DFE}=\widehat{DFz'}$. Mà $\widehat{DFE} = 110^{\circ}$ nên $\widehat{DFz'} = 110^{\circ}$ và do $\widehat{DFz'} = \widehat{BDy'}$ nên yy'//zz'.

b)
Cách 1: Với yy'//zz', ta có hai góc $\widehat{uEz'}, \widehat{uCy'}$ là hai góc trực góc cùng tại E nên ut $\perp $zz'.

Cách 2: Ta có $\widehat{uEz'}=90^{\circ}$ (góc vuông) và $\widehat{uCy'}=90^{\circ}$ (do yy'//zz') nên ut $\perp $zz'.

c)
Cách 1: Ta có $\widehat{uAx'}=\widehat{uEz'}$ (cùng chắn hai vòng cung) và cùng ở vị trí đồng vi nên xx'//zz'.

Cách 2: Với xx'//zz', ta có $\widehat{uAx'}=\widehat{uEz'}$ (hai góc trực góc) nên xx'//zz'.

Đáp án:
a) yy'//zz'
b) ut $\perp $zz'
c) xx' // zz'