1.PHƯƠNG PHÁP QUY NẠP TOÁN HỌCHoạt động 1: Hãy quan sát các đẳng thức sau:Có nhận xét gì về các số...
Câu hỏi:
1.PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Hoạt động 1: Hãy quan sát các đẳng thức sau: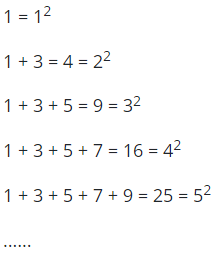
Có nhận xét gì về các số ở vế trái và ở vế phải của các đẳng thức trên? Từ đó hãy dự đoán công thức tính tổng của n số lẻ đầu tiên 1 + 3 + 5 + ... + (2n –1).
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
Phương pháp giải:Bước 1: Ta quan sát các đẳng thức đã cho và nhận thấy rằng vế trái của các đẳng thức lần lượt là tổng của 1, 2, 3, 4, 5, ... số lẻ đầu tiên. Còn vế phải lần lượt là bình phương của 1, 2, 3, 4, 5,...Bước 2: Dựa vào nhận xét trên, ta có thể dự đoán công thức tổng của n số lẻ đầu tiên 1 + 3 + 5 + ... + (2n – 1) là n^2.Câu trả lời của câu hỏi:Ta có công thức tổng của n số lẻ đầu tiên là: 1 + 3 + 5 + ... + (2n – 1) = n^2.
Câu hỏi liên quan:
- Hoạt động 2:Xét đa thức p(n) = n2– n +41.a)Hãy tính p(1), p(2), p(3), p(4),...
- Luyện tập 1:Chứng minh rằng với mọi số tự nhiên n≥ 1, ta có
- Luyện tập 2:Chứng minh rằng với mọi số tự nhiên n≥ 2, ta có đằng thức:
- 2.MỘT SỐ ỨNG DỤNG KHÁC CỦA PHƯƠNG PHÁP QUY NẠP TOÁN HỌCVận dụng:Lãi suất gửi tiết kiệm trong...
- BÀI TẬP2.1.Sử dụng phương pháp quy nạp toán học, chứng minh các đẳng thức sau đúng với mọi số tự...
- 2.2.Mỗi khẳng định sau là đủng hay sai? Nếu em nghĩ là nó đủng, hãy chứng minh nó. Nếu em...
- 2.3.Chứng minh rằng$n^{3}$– n + 3 chia hết cho 3 với mọi số tự nhiên n ≥ 1.
- 2.4.Chứng minh rằng$n^{2}$– n + 41 là số lẻ với mọi số nguyên dương n.
- 2.5.Chứng minh rằng nếu x > –1 thì$(1+x)^{n}$≥ 1+ nx với mọi số tự nhiên n.
- 2.6.Cho tổnga) Tính S1, S2, S3.b) Dự đoán công thức tính tồng Snvà chứng minh bằng quy...
- 2.7.Sừ dụng phương pháp quy nạp toán học, chứng minh rằng số đường chéo của một đa giác n cạnh (n ≥...
- 2.8.Ta sẽ “lập luận” bằng quy nạp toán học đề chỉ ra rằng: “Mọi con mèo đều có cùng màu”. Ta gọi...
Bình luận (0)





