Khám phá 3 trang 9 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hai hình hộp chữ nhật A và...
Câu hỏi:
Khám phá 3 trang 9 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hai hình hộp chữ nhật A và B có các kích thước như Hình 3.
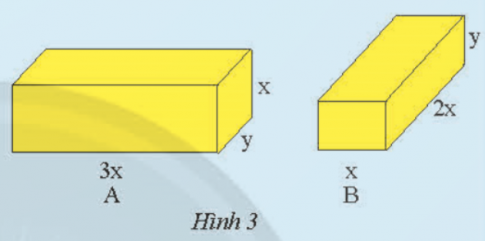
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
Để tính tổng thể tích của hai hình hộp chữ nhật A và B, ta cần tính thể tích của từng hình hộp rồi cộng lại.
a) Thể tích của hình hộp chữ nhật A được tính bằng công thức thể tích hình hộp chữ nhật: dài x rộng x cao. Với kích thước đã cho, ta có thể tích của hình hộp chữ nhật A là: 3x.y.x = 3x$^{2}$y (đơn vị thể tích).
Thể tích của hình hộp chữ nhật B cũng được tính tương tự: x.2x.y = 2x$^{2}$y (đơn vị thể tích).
Vậy, tổng thể tích của hình hộp chữ nhật A và B là: 3x$^{2}$y + 2x$^{2}$y = 5x$^{2}$y (đơn vị thể tích).
b) Để viết biểu thức biểu diễn sự chênh lệch thể tích của A và B, ta trừ thể tích của hình hộp chữ nhật A cho thể tích của hình hộp chữ nhật B.
Biểu thức chênh lệch thể tích của A và B là: 3x$^{2}$y – 2x$^{2}$y = (3 - 2)x$^{2}$y = x$^{2}$y (đơn vị thể tích).
Vậy, biểu thức biểu diễn sự chênh lệch thể tích của A và B là x$^{2}$y (đơn vị thể tích).
a) Thể tích của hình hộp chữ nhật A được tính bằng công thức thể tích hình hộp chữ nhật: dài x rộng x cao. Với kích thước đã cho, ta có thể tích của hình hộp chữ nhật A là: 3x.y.x = 3x$^{2}$y (đơn vị thể tích).
Thể tích của hình hộp chữ nhật B cũng được tính tương tự: x.2x.y = 2x$^{2}$y (đơn vị thể tích).
Vậy, tổng thể tích của hình hộp chữ nhật A và B là: 3x$^{2}$y + 2x$^{2}$y = 5x$^{2}$y (đơn vị thể tích).
b) Để viết biểu thức biểu diễn sự chênh lệch thể tích của A và B, ta trừ thể tích của hình hộp chữ nhật A cho thể tích của hình hộp chữ nhật B.
Biểu thức chênh lệch thể tích của A và B là: 3x$^{2}$y – 2x$^{2}$y = (3 - 2)x$^{2}$y = x$^{2}$y (đơn vị thể tích).
Vậy, biểu thức biểu diễn sự chênh lệch thể tích của A và B là x$^{2}$y (đơn vị thể tích).
Câu hỏi liên quan:
- 1. Đơn thức và đa thứcThực hành 1 trang 7 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho các...
- Vận dụng 1 trang 7 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một bức tường hình thang có cửa sổ...
- 2. Đơn thức thu gọnThực hành 2 trang 9 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thu gọn các đơn...
- 3. Cộng, trừ đơn thức đồng dạngThực hành 3 trang 10 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mỗi...
- 4. Đa thức thu gọnThực hành 4 trang 10 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thu gọn và tìm...
- Thực hành 5 trang 10 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính giá trị của đa thức...
- Vận dụng 2 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình hộp chữ nhật có các kích...
- Bài tậpBài tập 1 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Chỉ ra các đơn thức, đa thức...
- Bài tập 2 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thu gọn các đơn thức sau. Chỉ ra hệ...
- Bài tập 3 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thu gọn và tìm bậc của mỗi đa thức...
- Bài tập 4 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính giá trị của đa thức...
- Bài tập 5 trang 11 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Viết biểu thức biểu thị thể tích V...
- Khởi động trang 6 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình bên là bản vẽ sơ lược nền...
- Khám phá 1 trang 6 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Một số biểu thức được phân chia...
- Khám phá 2 trang 8 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Để tính thể tích của hình hộp...
- Khám phá 4 trang 6 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hai đa thức A =...






c) Một cách khác, ta cũng có thể viết biểu thức chênh lệch thể tích của hai hình hộp chữ nhật A và B bằng: |(a-x)*(b-y)*(c-z)|.
b) Để viết biểu thức biểu diễn sự chênh lệch thể tích của hai hình hộp chữ nhật A và B, ta tính sự chênh lệch giữa thể tích của A và thể tích của B: |(a*b*c) - (x*y*z)|.
a) Tổng tổ tích của hai hình hộp chữ nhật A và B được tính bằng tổng các thể tích của hai hình hộp chữ nhật đó. Với A có kích thước abc và B có kích thước xyz, tổng thể tích là: (a*b*c) + (x*y*z).