Câu 5: Trang 43 sách VNEN 9 tập 1Xác định hệ số góc của các đường thẳng cho trên hình 7.
Câu hỏi:
Câu 5: Trang 43 sách VNEN 9 tập 1
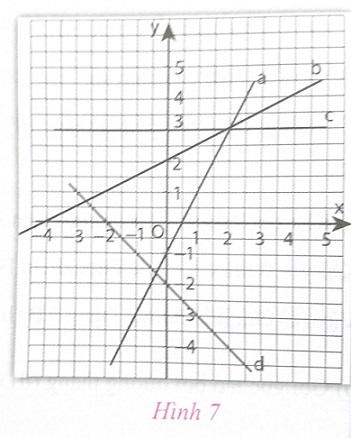
Xác định hệ số góc của các đường thẳng cho trên hình 7.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ánh
Để xác định hệ số góc của các đường thẳng trên hình 7 trang 43 sách VNEN 9 tập 1, ta cần biết rằng hệ số góc của một đường thẳng là tỷ số giữa độ dốc của đường thẳng đó và trục hoành.Để xác định hệ số góc của một đường thẳng, ta cần tìm đạo hàm của đường thẳng và từ đó suy ra hệ số góc.Ví dụ: Đường thẳng y = 2x - 1, đạo hàm của đường thẳng này sẽ là 2, tức là hệ số góc của đường thẳng là 2.Trả lời:1. Đường thẳng y = 2x - 1 có hệ số góc là 2.2. Đường thẳng y = 0,5x + 2 có hệ số góc là 0.5.3. Đường thẳng y = 3 có hệ số góc là 0.4. Đường thẳng y = -x - 2 có hệ số góc là -1.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 43 sách VNEN 9 tập 1Xác định hệ số góc của các đường thẳng...
- Câu 2: Trang 43 sách VNEN 9 tập 1Cho hàm số bậc nhất y = ax + 1.a) Xác định hệ số góc a, biết rằng...
- Câu 3: Trang 43 sách VNEN 9 tập 1Xác định giá trị của b, biết đồ thị hàm số y = 7x + b đi qua...
- Câu 4: Trang 43 sách VNEN 9 tập 1a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số:y...
- D. HOẠT ĐỘNG VẬN DỤNGCâu 1: Trang 44 sách VNEN 9 tập 1Với giá trị nào của k, đồ thị hàm số y = kx +...






Vì vậy, để giải câu hỏi này, ta cần xác định góc tạo bởi mỗi đường thẳng với trục hoành trên hình 7 và sau đó tính hệ số góc của từng đường thẳng đó bằng cách tính tangent của góc đó.
Để xác định hệ số góc của đường thẳng, ta cần xác định góc tạo bởi đường thẳng đó với trục hoành trong hình 7, sau đó tính tangent của góc đó để có hệ số góc tương ứng.
Trong trường hợp các đường thẳng này không song song với trục hoành, hệ số góc sẽ làm hệ số góc của đường thẳng chính là tangent của góc tạo bởi đường thẳng đó với trục hoành.
Để xác định hệ số góc của các đường thẳng trên hình 7, ta cần biết rằng hệ số góc của một đường thẳng được xác định bằng cách tính giá trị của góc tạo bởi đường thẳng đó với trục hoành.