C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 121 sách VNEN 9 tập 1Trên hình 127, hai đường tròn tiếp xúc tại...
Câu hỏi:
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 121 sách VNEN 9 tập 1
Trên hình 127, hai đường tròn tiếp xúc tại A.
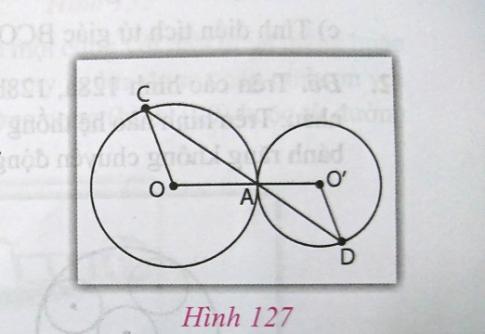
Chứng minh rằng $\Delta $OAC đồng dạng với $\Delta $O'AD.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
Để chứng minh rằng $\Delta OAC$ đồng dạng với $\Delta O'AD$, ta có thể làm theo các bước sau:1. Chứng minh các tam giác cân tại O: Ta có OA = OC nên tam giác OAC là tam giác cân tại O. Tương tự, O'A = O'D nên tam giác O'AD cũng là tam giác cân tại O.2. Chứng minh các góc của hai tam giác: Ta có $\widehat{OAC} = \widehat{O'AD}$ (do là các góc đối) nên $\widehat{AOC} = \widehat{AO'D}$.3. Chứng minh tỉ lệ đồng dạng: Với các cạnh và góc đã biết, ta có $\frac{O'A}{OA} = \frac{O'D}{OC}$ nên ta có thể kết luận được rằng $\Delta OAC$ đồng dạng với $\Delta O'AD$.Vậy, $\Delta OAC$ đồng dạng với $\Delta O'AD$.
Câu hỏi liên quan:
- Câu 2: Trang 121 sách VNEN 9 tập 1Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O;...
- Câu 3: Trang 121 sách VNEN 9 tập 1Cho đường tròn tâm O bán kính OA và O' là trung điểm của OA. Vẽ...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 1: Trang 122 sách VNEN 9 tập 1Cho hai đường tròn (O)...
- Câu 2: Trang 122 sách VNEN 9 tập 1Đố: Trên các hình 128a, 128b, 128c, các bánh xe tròn có răng cưa...






Đây là cách chứng minh sự đồng dạng giữa hai tam giác được gặp phổ biến trong lớp 9.
Từ đó, ta kết luận được rằng tam giác OAC đồng dạng với tam giác O'AD.
Vậy tỉ số các cạnh của tam giác OAC và tam giác O'AD là bằng nhau, từ đó suy ra hai tam giác này đồng dạng.
Ta cũng có O'C song song với O'D và góc AOC bằng góc ADO' (do cùng là góc nhìn từ trục thẳng CO và DO').
Gọi M là trung điểm của AD, ta có OA song song với O'M và góc AOM bằng góc O'AD (do cùng là góc nhìn từ trục thẳng MO và M'O').