Bài tập 3.23.Trên mặt phẳng toạ độ Oxy lấy điểm y M thuộc nửa đường tròn đơn vị, sao cho...
Câu hỏi:
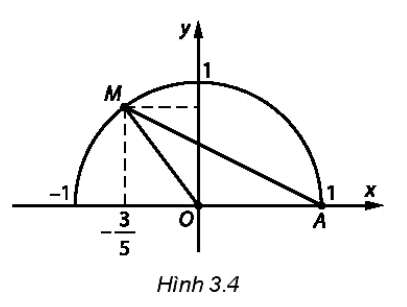
Bài tập 3.23. Trên mặt phẳng toạ độ Oxy lấy điểm y M thuộc nửa đường tròn đơn vị, sao cho $\widehat{xOM} = \frac{-3}{5}$ (H.3.4)
Diện tích của tam giác AOM bằng
A. $\frac{4}{5}$. B. $\frac{2}{5}$.
C. $\frac{3}{5}$. D. $\frac{3}{10}$.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hưng
Để giải bài toán này, ta sẽ thực hiện các bước sau:Bước 1: Vẽ đồ thị như sau: Với đường tròn đơn vị có tâm O(0,0) và yểm M thuộc nửa đường tròn.Bước 2: Gọi A là điểm có hoành độ x, ta có $\overrightarrow{OM} = (\cos(\frac{-3\pi}{5}), \sin(\frac{-3\pi}{5})) = (\cos(\frac{2\pi}{5}), -\sin(\frac{2\pi}{5}))$.Suy ra, $\overrightarrow{OA} = (\cos(\frac{2\pi}{5}) - x, -\sin(\frac{2\pi}{5}))$.Bước 3: Diện tích tam giác AOM bằng $\frac{1}{2} |\overrightarrow{OA} \times \overrightarrow{OM}|$.Thay các giá trị vào ta được diện tích tam giác AOM bằng $\frac{1}{2} |\sin(\frac{2\pi}{5}) + x \sin(\frac{2\pi}{5})| = \frac{1}{2} |\sin(\frac{2\pi}{5}) (1+x)|$.Bước 4: Ta cần tìm x sao cho diện tích tam giác AOM bằng $\frac{2}{5}$.Suy ra ta có phương trình $\frac{1}{2} |\sin(\frac{2\pi}{5}) (1+x)| = \frac{2}{5}$.Giải phương trình trên ta được x = 0 hoặc x = -1.Do đó, diện tích của tam giác AOM bằng $\frac{2}{5}$.Vậy câu trả lời đúng là: B. $\frac{2}{5}$.
Câu hỏi liên quan:
- Bài tập 3.17. Tam giác ABC có $\widehat{A} = 15^{o}$, $\widehat{B} = 45^{o}$. Giá trị của tanC...
- Bài tập 3.18. Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho...
- Bài tập 3.19. Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho...
- Bài tập 3.20.Cho góc nhọn $\alpha$ có tan $\alpha =\frac{3}{4}$. Giá trị của tích...
- Bài tập 3.21. Cho góc $\alpha$ ($0^{o} < \alpha < 180^{o}$) thoả mãn sin$\alpha$ +...
- Bài tập 3.22. Cho góc $\alpha$ thoả mãn sin$\alpha$ + cos$\alpha$ = $\sqrt{2}$. Giá trị của...
- Bài tập 3.24. Trên mặt phẳng toạ độ Oxy lấy điểm M thuộc nửa đường tròn đơn vị, sao cho...
- Bài tập 3.25. Cho cos$\alpha =\frac{1}{4}$. Giá trị của P = $\frac{tan\alpha +...
- Bài tập 3.26. Tam giác ABC có a = 2, b = 3, c = 4. Bán kính đường tròn ngoại tiếp của tam giác ABC...
- Bài tập 3.27.Tam giác ABC có a = 4, b = 5, c = 6. Độ dài đường cao $h_{b}$ bằngA....
- Bài tập 3.28. Cho tam giác ABC có a = 20, b = 16 và $m_{a}$ = 10. Diện tích của tam giác bằngA....
- Bài tập 3.29. Tam giác ABC có a = 14 b = 9 và $m_{a}$ = 8. Độ dài đường cao $h_{a}$bằngA....
- Bài tập 3.30. Tam giác ABC có $\widehat{A} = 45^{o}$, c = 6, $\widehat{B} = 75^{o}$.Độ dài đường...
- Bài tập 3.31. Tam giác ABC có $\widehat{A} = 45^{o}$, c = 6, $\widehat{A} = 75^{o}$.Độ dài bán kính...
- Bài tập 3.23. Tam giác ABC có diện tích S = $2R^{2}$.sinBsinC, với R là độ đài bán kính đường tròn...
- Bài tập 3.33. Tam giác ABC có AB = $\sqrt{5}$, AC = $\sqrt{2}$ và $\widehat{C} = 45^{o}$Độ dài cạnh...
- Bài tập 3.34. Tam giác ABC có $\widehat{C} = 60^{o}$, AC = 2 và AB = $\sqrt{2}$.Diện tích của tam...
- Bài tập 3.35. Tam giác ABC có $\widehat{A} = 60^{o}$, AB = 3 và BC = $3\sqrt{3}$.Độ dài bán kính...
- Bài tập 3.36. Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 60 km/h. Cùng lúc đó,...
- Bài tập 3.37. Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6 m so với...
- Bài tập 3.38. Cho góc tù $\alpha$ có sin$\alpha = \frac{1}{3}$a) Tính cos$\alpha$, tan$\alpha$,...
- Bài tập 3.39. Cho $sin15^{o} = \frac{\sqrt{6}-\sqrt{2}}{4}$a) Tính $sin75^{o}$, $cos105^{o}$,...
- Bài tập 3.40. Cho tam giác ABC có AB = 1, BC = 2 và $\widehat{ABC} = 60^{o}$. Tính độ dài cạnh và...
- Bài tập 3.41. Cho tam giác ABC có c = 1, a = 2 và $\widehat{B} = 120^{o}$.a) Tính b, $\widehat{A}$,...
- Bài tập 3.42. Cho tam giác ABC có a = 3, b = 5 và c = 7.a) Tính các góc của tam giác, làm tròn đến...
- Bài tập 3.43. Cho tam giác ABC có $\widehat{B} = 45^{o}$ , $\widehat{C} = 15^{o}$ và b =...
- Bài tập 3.44. Cho tam giác ABC, có c = 5, a = 8 và $\widehat{B} = 60^{o}$.a) Tính b và số đo các...
- Bài tập 3.45. Cho tam giác ABC có $\widehat{B} = 15^{o}, \widehat{C} = 30^{o}$ và c = 2.a) Tính số...
- Bài tập 3.46. Trên biển, một tàu cá xuất phát từ cảng A, chạy về phương đông 15 km tới B, rồi...
- Bài tập 3.47. Trên sườn đồi, với độ dốc 12% (độ dốc của sườn đồi được tính bằng tang của góc nhọn...
Bình luận (0)





