Bài 12: Ở hình 20 có hai góc AOB và BOC là hai góc kề bù, $\widehat{AOB}=3\widehat{BOC}...
Câu hỏi:
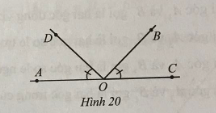
Bài 12: Ở hình 20 có hai góc AOB và BOC là hai góc kề bù, $\widehat{AOB}=3\widehat{BOC}, \widehat{AOD}=\widehat{BOC}$
a) Tính số đo góc BOC.
b) Tia OB có là tia phân giác góc COD hay không?
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
a) Ta có $\widehat{AOB}+\widehat{BOC}=180^{\circ}$ (hai góc kề bù)Mà $\widehat{AOB}=3\widehat{BOC}$ nên $3\widehat{BOC}+\widehat{BOC}=4\widehat{BOC}=180^{\circ}$ hay $\widehat{BOC}=45^{\circ}$.b) Do $\widehat{AOD}=\widehat{BOC}$ nên $\widehat{AOD}=45^{\circ}$.Ta có hai góc BOD và BOC là hai góc kề nhau nên $\widehat{COD}=\widehat{BOD}+\widehat{BOC}$.Mà $\widehat{AOD}+\widehat{COD}=180^{\circ}$ (hai góc kề bù) nên $\widehat{AOD}+\widehat{BOD}=180^{\circ}$.Suy ra $\widehat{BOD}=180^{\circ}-\widehat{AOD}-\widehat{BOC}=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$.Do đó hai góc BOD và BOC không bằng nhau.Vậy OB không là tia phân giác của góc COD.Đáp án:a) $\widehat{BOC}=45^{\circ}$b) OB không là tia phân giác của góc COD.
Câu hỏi liên quan:
- BÀI TẬPBài 8: Ở hình 16 có $\widehat{xOz}=40^{\circ};\widehat{xOy}=80^{\circ}$. Tia Oz có là...
- Bài 9: Ở hình 17 có On, Oq lần lượt là tia phân giác của góc mOp, pOr. Tính số đo mỗi góc mOr, pOq,...
- Bài 10: Ở hình 18 có$ \widehat{xOM}=\widehat{yON}=30^{\circ}$, OI là tia phân giác góc MON. Hai...
- Bài 11: Ở hình 19 có $\widehat{COD}=80^{\circ},\widehat{COE}=60^{\circ}$, tia OG là tia phân...
- Bài 13: Ở hình 21 có $\widehat{xOy}=70^{\circ},\widehat{xOz}=120^{\circ}$, hai tia OM và ON...
- Bài 14: Ở hình 22 có $\widehat{AOB}=60^{\circ}$, tia OC là tia phân giác góc AOB.a) Tính số đo góc...
- Bài 15: Ở hình 23 có $\widehat{BOC}=42^{\circ},\widehat{AOD}=97^{\circ},\widehat{AOE}=56^{\circ}$a)...






{"content1": "a) Từ điều kiện hai góc kề bù, ta có $\widehat{AOB} + \widehat{BOC} = 180^{\circ}$. Vì $\widehat{AOB}=3\widehat{BOC}$, nên thay vào ta được $3\widehat{BOC} + \widehat{BOC} = 180^{\circ} \Rightarrow 4\widehat{BOC} = 180^{\circ} \Rightarrow \widehat{BOC} = 45^{\circ}$. Do đó, số đo góc BOC là 45 độ.","content2": "b) Tia OB có là tia phân giác góc COD hay không, ta cần kiểm tra xem góc AOD có bằng góc BOC không. Ta đã biết $\widehat{AOD}=\widehat{BOC}=45^{\circ}$ nên góc AOD bằng góc BOC. Vì vậy, tia OB chính là tia phân giác góc COD.","content3": "Vậy số đo góc BOC là 45 độ và tia OB chính là tia phân giác góc COD."}