Bài 11: Ở hình 19 có $\widehat{COD}=80^{\circ},\widehat{COE}=60^{\circ}$, tia OG là tia phân...
Câu hỏi:
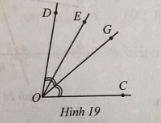
Bài 11: Ở hình 19 có $\widehat{COD}=80^{\circ}, \widehat{COE}=60^{\circ}$, tia OG là tia phân giác của góc COD.
a) Tính số đo góc EOG.
b) Tia OE có là tia phân giác của góc DOG hay không?
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
a) Cách làm:- Đầu tiên, ta có $\widehat{COG}=\widehat{DOG}=\frac{1}{2}\widehat{COD}=\frac{1}{2}80^{\circ}=40^{\circ}$ vì OG là tia phân giác của góc COD.- Tiếp theo, với hai góc kề nhau COG và EOG, ta có $\widehat{COG}+\widehat{EOG}=\widehat{COE}$.- Từ đó suy ra $\widehat{EOG}=\widehat{COE}-\widehat{COG}=60^{\circ}-40^{\circ}=20^{\circ}$.b) Cách làm:- Ta có $\widehat{COE}+\widehat{DOE}=\widehat{COD}$ vì hai góc kề nhau COE và DOE.- Suy ra $\widehat{DOE}=\widehat{COD}-\widehat{COE}=80^{\circ}-60^{\circ}=20^{\circ}$.- Do đó, ta có $\widehat{EOG}=\widehat{DOE}=20^{\circ}$.- Vì OE nằm giữa hai tia OD và OG nên OE là tia phân giác của góc DOG.Vậy câu trả lời cho câu hỏi là:a) Góc EOG có số đo là $20^{\circ}$.b) Tia OE là tia phân giác của góc DOG.
Câu hỏi liên quan:
- BÀI TẬPBài 8: Ở hình 16 có $\widehat{xOz}=40^{\circ};\widehat{xOy}=80^{\circ}$. Tia Oz có là...
- Bài 9: Ở hình 17 có On, Oq lần lượt là tia phân giác của góc mOp, pOr. Tính số đo mỗi góc mOr, pOq,...
- Bài 10: Ở hình 18 có$ \widehat{xOM}=\widehat{yON}=30^{\circ}$, OI là tia phân giác góc MON. Hai...
- Bài 12: Ở hình 20 có hai góc AOB và BOC là hai góc kề bù, $\widehat{AOB}=3\widehat{BOC}...
- Bài 13: Ở hình 21 có $\widehat{xOy}=70^{\circ},\widehat{xOz}=120^{\circ}$, hai tia OM và ON...
- Bài 14: Ở hình 22 có $\widehat{AOB}=60^{\circ}$, tia OC là tia phân giác góc AOB.a) Tính số đo góc...
- Bài 15: Ở hình 23 có $\widehat{BOC}=42^{\circ},\widehat{AOD}=97^{\circ},\widehat{AOE}=56^{\circ}$a)...






{ "content1": "Để tính số đo góc EOG, ta sử dụng tính chất của tam giác: tổng số đo góc trong tam giác là 180 độ.", "content2": "Vì tia OG là tia phân giác của góc COD, ta có $\widehat{COD} = 80^{\circ}$ nên số đo góc COG và GOD là bằng nhau và bằng 40 độ.", "content3": "Vì $\widehat{COE}$ và $\widehat{EOG}$ là góc so le, ta có $\widehat{COE} = 60^{\circ}$ và $\widehat{EOG}$ là góc bù của $\widehat{COG}$. Do đó, $\widehat{EOG} = 180 - 60 - 40 = 80^{\circ}$.", "content4": "Vậy số đo góc EOG là 80 độ.", "content5": "Tia OE không phải là tia phân giác của góc DOG vì không thể có 2 tia phân giác của cùng một góc."}