Thực hành 2: Giải các hệ phương trình sau bằng phương pháp Gauss:
Câu hỏi:
Thực hành 2: Giải các hệ phương trình sau bằng phương pháp Gauss:
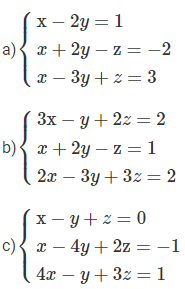
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Linh
Phương pháp giải hệ phương trình bằng phương pháp Gauss:1. Đưa hệ phương trình về dạng ma trận tương đương: $\begin{cases} x + 2y + z = 1 \\ 3x + 6y + 5z = 5 \end{cases}$Ta có ma trận tương ứng: $\begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 3 & 6 & 5 & | & 5 \end{pmatrix}$2. Thực hiện biến đổi để ma trận trở thành dạng bậc thang:$\begin{array}{lcl} Row_{2} = Row_{2} - 3 \cdot Row_{1} & \Rightarrow & \begin{pmatrix} 1 & 2 & 1 & | & 1 \\ 0 & 0 & 2 & | & 2 \end{pmatrix}\end{array}$3. Giải hệ phương trình sau khi đưa ma trận về dạng bậc thang: $\begin{cases} 2z = 2 \\ x + 2y + z = 1 \end{cases}$4. Từ phương trình đầu tiên, suy ra z = 1. Thay vào phương trình thứ hai, ta được x + 2y + 1 = 1 hay x + 2y = 0, tức là x = -2y. Vậy hệ phương trình đã cho có vô số nghiệm và nghiệm của nó là dạng (-2y + 1; y; 1).
Câu hỏi liên quan:
- 1.ĐỊNH NGHĨA HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨNHoạt động khám phá 1:Ba lớp 10A, 10B, 10C gồm 128...
- Thực hành 1:Hệ phương trình nào dưới đây là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số (1;...
- 2.GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN BẰNG PHƯƠNG PHÁP GAUSSHoạt động khám phá 2: Cho hệ phương...
- Vận dụng 1: Tìm phương trình của parabol (p):y = $ax^2$ + bx + c (a ≠ 0), biết (P) đi...
- 3.SỬ DỤNG MÁY TÍNH CẦM TAY TÌM NGHIỆM CỦA HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨNThực hành 3: Sử dụng máy...
- Vận dụng 2:Ba bạn Nhân, Nghĩa và Phúc đi vào căng tin của trường. Nhân mua một li trà sữa,...
- BÀI TẬP1.Trong các hệ phương trình sau, hệ nào là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba...
- 2. Giải các hệ phương trình sau bằng phương pháp Gauss
- 3. Sử dụng máy tính cầm tay, tìm nghiệm của các hệ phương trình sau:
- 4. Tìm phương trình của Parabol (P): y= $ax^2$ + bx + c (a ≠ 0), biết:a) Parabol (P) có trục đối...
- 5.Một đại lí bán ba loại gas A, B, C với giá bán mỗi bình gas lần lượt là 520000 đồng, 480000...
Bình luận (0)





