Ôn thi lên lớp 10 môn Toán Chuyên đề Diện tích đa giác
Chuyên đề Diện tích đa giác
Chuyên đề này là kết quả của quá trình học tập và nghiên cứu về đa giác. Hy vọng rằng nó sẽ giúp bạn hiểu rõ hơn về kiến thức này và vượt qua các thách thức trong học tập môn Toán. Dưới đây là một số kiến thức cơ bản về diện tích đa giác:
- Đa giác lồi: Đa giác nếu không có góc nào lớn hơn 180 độ.
- Đa giác đều: Đa giác có các cạnh và góc đều nhau.
- Tổng các góc trong đa giác n cạnh là: $(n – 2) \times 180^{\circ}$.
- Số đường chéo của một đa giác n cạnh là: $\frac{(n-3)n}{2}$.
- Tổng các góc ngoài của một đa giác n cạnh là: $360^{\circ}$.
- Diện tích tam giác: $\frac{1}{2} \times a \times h$ (a: cạnh đáy, h: chiều cao tương ứng).
- Diện tích hình chữ nhật: $S = a \times b$.
Đây chỉ là một phần nhỏ trong chuyên đề Diện tích đa giác. Hy vọng rằng bạn sẽ tìm thấy nó hữu ích và sẽ áp dụng kiến thức này vào việc giải các bài tập thực hành.
Bài tập và hướng dẫn giải
Bài 1: Cho hình thang ABCD, đáy AB = 3cm, AD = 4cm, BC = 6cm, CD = 9cm. Tính diện tích hình thang .
Bài 2: Cho $\triangle ABC$ có chu vi là 2p, cạnh BC = a, gọi góc $\widehat{BAC}=\alpha $ , đường tròn nội tiếp tam giác ABC tiếp xúc cạnh AC tại K.
Tính diện tích $\triangle AOK$ .
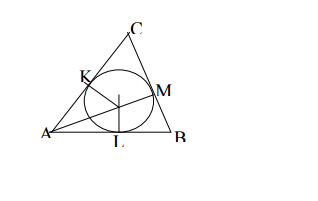
Bài 3: Cho $\triangle ABC$ . Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}$ . Gọi O là giao điểm của BN và CM.
Gọi H, L lần lượt là chân đường vuông góc kẻ từ A, C tới đường thẳng BN.
a/ Chứng minh CL = 2 AH.
b/ Chứng minh: $S_{BOC} = 2S_{BOA}$ .
Kẻ CE và BD vuông góc với AO. Chứng minh BD = CE.
c/ Giả sử $S_{ABC} = 20 cm^{2}$ , tính $S_{AMON}$ .
Bài 4: Cho hình thang ABCD, đáy AB, O là giao điểm của hai đường chéo AC và BD.
a. Chứng minh rằng: $S_{OAD}=S_{OBC}$ .
b. $S_{OAB}.S_{OCD}=(S_{OBC})^{2}$ .
Bài 5: Cho $\triangle ABC$ biết : $\widehat{A}=\alpha ,\widehat{B}=\beta ,\widehat{C}=\delta $, đường tròn nội tiếp tam giác có bán kính bằng r. P, Q, R là các tiếp điểm. Tính diện tích tam giác PQR .





