Bài 2:Cho $\triangle ABC$ có chu vi là 2p, cạnh BC = a, gọi góc...
Câu hỏi:
Bài 2: Cho $\triangle ABC$ có chu vi là 2p, cạnh BC = a, gọi góc $\widehat{BAC}=\alpha $ , đường tròn nội tiếp tam giác ABC tiếp xúc cạnh AC tại K.
Tính diện tích $\triangle AOK$ .
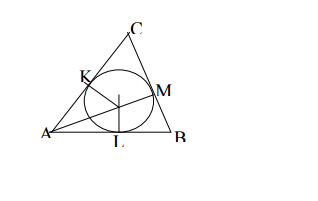
Câu trả lời:
Người trả lời: GV. Đỗ Thị Long
Để giải bài toán này, ta có thể sử dụng phương pháp tính diện tích tam giác bằng công thức \(S = \frac{1}{2}ab\sin C\).Gọi \(O\) là trung điểm của \(BC\), khi đó ta có \(AO\) là đường trung trực của tam giác \(ABC\), và từ đó ta có \(AK = AL\).Ta có \(AK = p - a\), và \(AO = \frac{a}{2}\).\(S_{AOK} = \frac{1}{2}AK \cdot AO = \frac{1}{2}(p - a)\cdot \frac{a}{2} = \frac{1}{2}\left(\frac{a(p-a)}{2}\right) = \frac{1}{2}\left(\frac{a(2p-a)}{2}\right) = \frac{a(p-a)}{4}\).Vậy diện tích của tam giác \(AOK\) là \(\frac{a(p-a)}{4}\).
Câu hỏi liên quan:
- Bài 1: Cho hình thang ABCD, đáy AB = 3cm, AD = 4cm, BC = 6cm, CD = 9cm. Tính diện...
- Bài 3: Cho $\triangle ABC$. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho...
- Bài 4: Cho hình thang ABCD, đáy AB, O là giao điểm của hai đường chéo AC và BD.a. Chứng minh...
- Bài 5: Cho $\triangle ABC$ biết : $\widehat{A}=\alpha ,\widehat{B}=\beta ...






Để tính được diện tích tam giác AOK, ta cần biết diện tích tam giác ABC. Có thể sử dụng công thức diện tích tam giác ABC = p*R, với R là bán kính đường tròn ngoại tiếp tam giác ABC và p là nửa chu vi tam giác ABC.
Ta có thể tính được AK bằng cách sử dụng công thức tính đường cao trong tam giác: AK = 2 * Diện tích tam giác ABC / BC = 2 * Diện tích tam giác ABC / a.
Vì đường tròn nội tiếp tam giác ABC tiếp xúc cạnh AC tại K nên ta có AK là đường cao của tam giác ABC. Do đó diện tích tam giác AOK sẽ bằng 1/2 * AK * AO.