Câu 4: Trang 138 toán VNEN tập 2Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm ), bán...
Câu 4: Trang 138 toán VNEN tập 2
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm ), bán kính R, có các đường cao AG, BF, CL cắt nhau tại H. Hơn nữa, AG, BF cắt (O) tương ứng tại D và E. Kẻ đường kính AJ. Gọi K là trung điểm của BC. Chứng minh rằng:
a) AFGB là tứ giác nội tiếp
b) BHD là tam giác cân
c) E và H đối xứng với nhau qua AC
d) K là trung điểm của đoạn thẳng HJ.
e) AH = 2OK.
Hướng dẫn: Xem hình 145
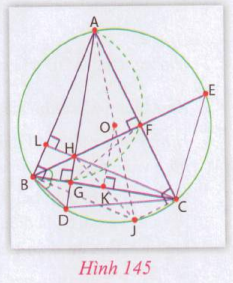
a) Do $\widehat{AFB} = \widehat{AGB} = 90^\circ$ nên AFGB là tứ giác nội tiếp. Suy ra, $\widehat{GAF} = \widehat{FBG}$ (*) (cùng chắn cung GF).
Lại có: $\widehat{CAD} = \widehat{CBD}$ (cùng chắn cung CD của (O)), nên BHD là tam giác cân. Với (O), từ (*) suy ra: cung CD = cung CE, nên CD = CE. Do đó, E và H $.......$
Do $\widehat{JBA} = 90^\circ$ (chắn nửa đường tròn) nên BJ // CL.
Tương tự, JC // BF nên BHCJ là hình bình hành, suy ra K là $.........$.
Do O và K tương ứng là trung điểm của JA và JH nên $................$
- C. Hoạt động luyện tậpCâu 1: Trang 134 toán VNEN 9 tập 2Thực hiện các hoạt động sauMột bạn hỏi, một...
- 3. Luyện tập, ghi vào vởCâu 1: Trang 137 toán VNEN 9 tập 2Xem hình 142 và cho biết tên của từng...
- Câu 2: Trang 137 toán VNEN 9 tập 2Xem hình 143 và cho biết diện tích phần tô đậm.Hướng dẫn: Phần tô...
- Câu 3: Trang 137 toán VNEN 9 tập 2Có ba bánh xe răng cưa A, B, C ăn khớp với nhau (h.144), cùng...
- Câu 5: Trang 138 toán VNEN 9 tập 2Cho đường tròn tâm O, bán kính R và một điểm A cố định trên đường...
- Câu 6: Trang 138 toán VNEN 9 tập 2Qua thăm dò ý kiến của 1080 học sinh thuộc một trường THCS về sở...






{1. Tứ giác AFGB là tứ giác nội tiếp vì có hai góc vuông tại A và B.2. Tam giác BHD là tam giác cân vì BD = CD (cùng bán kính của đường tròn nội tiếp).3. E và H đối xứng với nhau qua AC vì E là giao điểm của BF và (O), H là giao điểm của AG và (O).4. K là trung điểm của đoạn thẳng HJ vì HJ là đường chéo của hình bình hành BHCJ và K là trung điểm của BC.5. AH = 2OK vì O và K tương ứng là trung điểm của JA và JH nên theo định lí trung điểm ta có AH = 2OK.}