Câu 3: Trang 104 toán VNEN 9 tập 2a) Cho đường tròn (O) có hai dây AB và CD cắt nhau tại điểm E nằm...
Câu 3: Trang 104 toán VNEN 9 tập 2
a) Cho đường tròn (O) có hai dây AB và CD cắt nhau tại điểm E nằm trong đường tròn (O). Chứng minh rằng: $EA\times EB = EC\times ED$.
Hướng dẫn: Xem hình 83

Nối AD, BC khi đó $\widehat{DAB} = \widehat{DCB}$ (vì cùng chắn cung DB) và $\widehat{ADC} = \widehat{ABC}$ (vì cùng chắn cung $...$)
Do đó, DEA và BEC là hai tam giác đồng dạng.
Từ đó, suy ra: $\frac{DE}{BE} = \frac{...}{EC}$, hay $...$
b) Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm là A và B. Tiếp tuyến tại điểm A của đường tròn (O) cắt đường tròn (O') tại điểm C (khác với A). CB cắt (O) tại điểm D (khác với B). Gọi Cy là tiếp tuyến của (O') tại điểm C. Chứng minh Cy // AD.
Hướng dẫn: Xem hình 84

Trong (O') thì $\widehat{BCy}$ là góc tạo bởi tia tiếp tuyến Cy và dây cung BC, nên $\widehat{BCy} = \frac{1}{2} sd CB$, còn $\widehat{CAB}$ là góc nội tiếp chắn cung CB, nên $\widehat{CAB} = \frac{1}{2}CB$, suy ra $\widehat{BCy} = \widehat{CAB}$. Tương tự với (O), chứng minh được $\widehat{CAB} = \widehat{BDA}$.
Từ đó, suy ra: $...............$
c) Cho đường tròn (O; R) và dây cung HI. Qua điểm H kẻ Hx sao cho góc $\widehat{IHx}$ có số đo bằng nửa số đo cung nhỏ HI. Chứng minh rằng $OH \perp Hx$.
Hướng dẫn: Xem hình 85
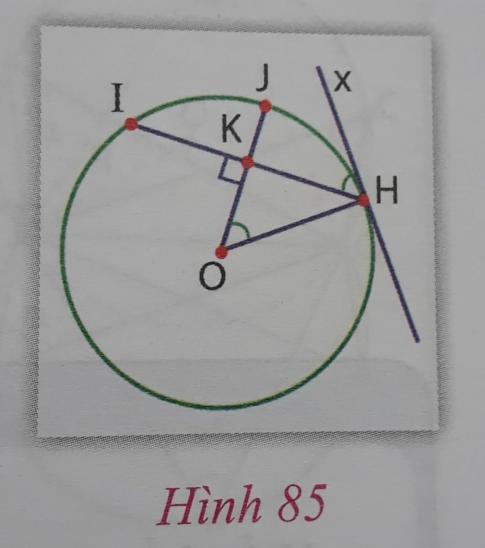
Gọi J là điểm chính giữa cung nhỏ HI và K là giao điểm của OJ với HI thì $OK \perp HK$ và $\widehat{KOH} = \frac{1}{2}sd HI$.
Theo giả thiết, $\widehat{IHx} = \frac{1}{2} sd IH$ nên $\widehat{IHx} = \widehat{KOH}$.
Do hai góc nhọn này đã có một cặp cạnh vuông góc với nhau ($OK \ perp HI$), nên $.................$ tức là $..................$
- C. Hoạt động luyện tập1. Thực hiện các hoạt động sau để ôn lại các kiến thức, kĩ năng đã họcCâu 1:...
- 2. Luyện tập, ghi vào vởCâu 1: Trang 104 toán VNEN 9 tập 2a) Xem hình 79, biết OIJ là tam giác đều,...
- Câu 2: Trang 104 toán VNEN 9 tập 2a) Cho hai đường tròn có tâm lần lượt là E và F cắt nhau tại hai...
- Câu 4: Trang 105 toán VNEN 9 tập 2Cho đường tròn (O; r) có đường kính MQ. Các điểm N, P cùng thuộc...






{ "content1": "a) Ta có $\frac{DE}{BE} = \frac{EA}{EB}$ và $\frac{EC}{CE} = \frac{EA}{EB}$, suy ra $DE \times EB = EA \times EC$.", "content2": "b) Ta có $\widehat{CAB} = \widehat{BCy}$ và $\widehat{CAB} = \widehat{BDA}$, từ đó suy ra Cy // AD.", "content3": "c) Ta có $\widehat{IHx} = \widehat{KOH}$ và $\widehat{IHx} = \widehat{KOH}$, do có một cặp góc vuông nên OH ⊥ Hx.", "content4": "d) Trong phần này của câu hỏi, bạn cần tự giải và trình bày lời giải của mình."}