2. Luyện tập, ghi vào vởCâu 1: Trang 104 toán VNEN 9 tập 2a) Xem hình 79, biết OIJ là tam giác đều,...
Câu hỏi:
2. Luyện tập, ghi vào vở
Câu 1: Trang 104 toán VNEN 9 tập 2
a) Xem hình 79, biết OIJ là tam giác đều, cho biết số đo của các góc nội tiếp cùng chắn cung IJ.
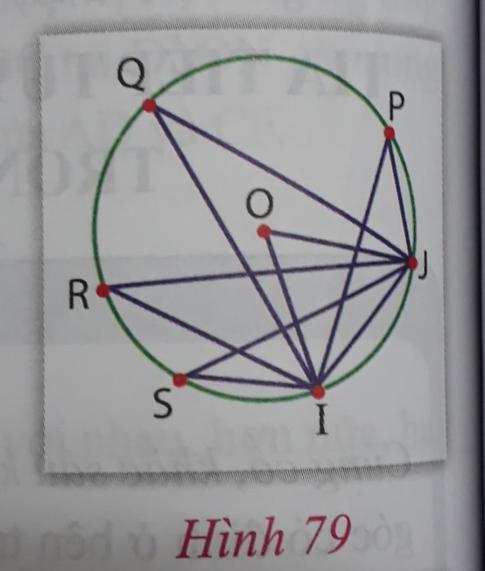
Hướng dẫn: Vì $\widehat{ISJ}$ là góc nội tiếp chắn cung nhỏ IJ có số đo là $60^\circ$ nên $\widehat{ISJ} = 30^\circ$.
$\widehat{IRJ} = ....;\; \widehat{IQJ} = ....;\; \widehat{IPJ} = ...$
b) Xem hình 80, biết OTJ là tam giác đều, cho biết số đo của mỗi góc sau đây: $\widehat{TYJ};\; \widehat{TOY};\;\widehat{TZY};\;\widehat{YTJ}$.

Hướng dẫn: Do OJT là tam giác đều nên cung nhỏ TJ có số đo là $60^\circ$, suy ra góc nội tiếp $\widehat{TYJ} = 30^\circ$.
$\widehat{TOY} = ...;\; \widehat{TZY} = ....; \;\widehat{YTJ} = ....$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ánh
Để giải bài toán trên, ta có thể thực hiện như sau:a) - Ta có góc nội tiếp chắn cung nhỏ IJ là $\widehat{ISJ} = 60^\circ$, suy ra $\widehat{ISJ} = 30^\circ$.- Vậy ta có: $\widehat{IRJ} = \widehat{ISJ} = 30^\circ$$\widehat{IQJ} = \widehat{ISJ} = 30^\circ$$\widehat{IPJ} = \widehat{ISJ} = 30^\circ$b) - Ta có cung nhỏ TJ trong tam giác đều OTJ có số đo $60^\circ$, từ đó suy ra $\widehat{TYJ} = 30^\circ$.- Từ đó, ta tính được:$\widehat{TOY} = 180^\circ - \widehat{IOT} = 180^\circ - 60^\circ = 120^\circ$$\widehat{TZY} = 60^\circ$ (góc nội tiếp chắn cung nhỏ TY)$\widehat{YTJ} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)Vậy, các câu trả lời là:a) $\widehat{IRJ} = 30^\circ ;\; \widehat{IQJ} = 30^\circ;\; \widehat{IPJ} = 30^\circ$b) $\widehat{TOY} = 120^\circ; \;\widehat{TZY} = 60^\circ;\;\widehat{YTJ} = 90^\circ$
Câu hỏi liên quan:
- C. Hoạt động luyện tập1. Thực hiện các hoạt động sau để ôn lại các kiến thức, kĩ năng đã họcCâu 1:...
- Câu 2: Trang 104 toán VNEN 9 tập 2a) Cho hai đường tròn có tâm lần lượt là E và F cắt nhau tại hai...
- Câu 3: Trang 104 toán VNEN 9 tập 2a) Cho đường tròn (O) có hai dây AB và CD cắt nhau tại điểm E nằm...
- Câu 4: Trang 105 toán VNEN 9 tập 2Cho đường tròn (O; r) có đường kính MQ. Các điểm N, P cùng thuộc...
Bình luận (0)





