Câu 2: Trang 76 sách VNEN 9 tập 1Ba vị trí M, N, P ở ba đỉnh của tam giác vuông, góc tại P là góc...
Câu hỏi:
Câu 2: Trang 76 sách VNEN 9 tập 1
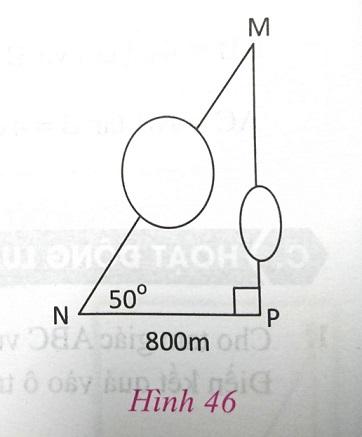
Ba vị trí M, N, P ở ba đỉnh của tam giác vuông, góc tại P là góc vuông (h.46). Khoảng cách giữa hai vị trí N và P là 800m. Góc tại đỉnh N là $50^{\circ}$. Giữa hai vị trí M và N có một cái vườn, giữa hai vị trí M và P có một cái ao. Em hãy cho biết khoảng cách giữa hai vị trí M và N, khoảng cách giữa hai vị trí M và P.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ngọc
Cách làm:Bước 1: Sử dụng định lý sin và cos trong tam giác vuông, ta có:cos$50^{\circ}$ = $\frac{NP}{MN}$$\Rightarrow$ MN = $\frac{NP}{cos50^{\circ}}$$\Rightarrow$ MN = $\frac{800}{cos50^{\circ}}$ = 1244 mBước 2: Sử dụng định lý Pythagoras trong tam giác vuông MNP:MP = $\sqrt{MN^2 - NP^2}$MP = $\sqrt{1244^2 - 800^2}$MP = $\sqrt{1547536 - 640000} = \sqrt{907536}$ = 952 mVậy khoảng cách giữa hai vị trí M và N là 1244m, khoảng cách giữa hai vị trí M và P là 952m.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 75 sách VNEN 9 tập 1Cho tam giác ABC vuông tại A (h.44).Điền kết...
- Câu 2: Trang 75 sách VNEN 9 tập 1Tính các cạnh và các góc còn lại của tam giác vuông ABC vuông tại...
- D. HOẠT ĐỘNG VẬN DỤNG và TÌM TOI, MỞ RỘNGCâu 1: Trang 76 sách VNEN 9 tập 1Foot (viết tắt là ft) là...






Khoảng cách giữa hai vị trí M và P được tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông MNP. Ta có MP^2 = MN^2 + NP^2
Khoảng cách giữa hai vị trí M và N là MN = 800 * cos(50) ≈ 513.71m
Với NP = 800m và góc(N) = 50 độ, ta có MN = 800 * cos(50)
Khoảng cách giữa hai vị trí M và N được tính bằng cách sử dụng định lý cosin trong tam giác vuông MNP. Ta có cos(N) = MN/NP = cos(50)