BÀI TẬPBài 16: Quan sát hình 28, biết a//b, $\widehat{M3}=50^{\circ}$a) Nêu những cặp góc so le...
Câu hỏi:
BÀI TẬP
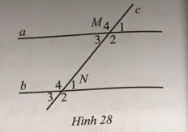
Bài 16: Quan sát hình 28, biết a//b, $\widehat{M3}=50^{\circ}$
a) Nêu những cặp góc so le trong, những cặp góc động vị
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hạnh
Để giải bài toán trên, ta có thể sử dụng các thông tin đã cho như sau:1. Vì a//b nên ta có:- Góc M1 và góc N1 lần lượt là góc đối và góc cận cạnh của tam giác M12N1.- Góc M2 và góc N2 lần lượt là góc đối và góc cận cạnh của tam giác M23N2.- Góc M3 và góc N3 lần lượt là góc đối và góc cận cạnh của tam giác M34N3.- Góc M4 và góc N4 lần lượt là góc đối và góc cận cạnh của tam giác M14N4.2. Ta có $\widehat{M3}=50^{\circ}$. Do góc nội tiếp trong cùng một cung có đo bằng nhau nên $\widehat{N1}=50^{\circ}$.3. Ta biết rằng góc trong tam giác bằng 180 độ nên:- $\widehat{M1}=180^{\circ}-\widehat{M3}=180^{\circ}-50^{\circ}=130^{\circ}$.- $\widehat{N3}=180^{\circ}-\widehat{M3}=180^{\circ}-50^{\circ}=130^{\circ}$.4. Từ a//b, ta có:- $\widehat{M1}=\widehat{M4}$ và $\widehat{N1}=\widehat{N4}$.- Tương tự, $\widehat{M2}=\widehat{M3}$ và $\widehat{N2}=\widehat{N3}$.Do đó, các câu trả lời cho bài toán là:a) Những cặp góc so le trong: M3 và N1, M2 và N4Những cặp góc đồng vị: M1 và N1, M4 và N4, M2 và N2, M3 và N3b) $\widehat{M1}=130^{\circ}$, $\widehat{M2}=130^{\circ}$, $\widehat{M4}=130^{\circ}$ $\widehat{N1}=50^{\circ}$, $\widehat{N3}=130^{\circ}$, $\widehat{N2}=130^{\circ}$, $\widehat{N4}=50^{\circ}$
Câu hỏi liên quan:
- Bài 17: Quan sát hình 29, biết a//b, $3\widehat{A1}=2\widehat{A2}$. Tìm số đo mỗi góc của đỉnh A và...
- Bài 18: Tìm số đo góc B1, B2, B3, B4 trong hình 30, biết m//n
- Bài 19: Quan sát hình 31, biết $\widehat{P3}=\widehat{Q1}=75^{\circ},\widehat{M3}=10...
- Bài 20: Tìm số đo x, y trong hình 32.
- Bài 21: Tìm số đo góc BCD trong hình 33.
- Bài 22. Quan sát hình 34, biết d1//d2 và góc tù tạo bởi đường thẳng a và đường thẳng d1 bằng 15...
- Bài 23: Quan sát hình 35, biết xx'//yy'//zz'. Chứng tỏ...
- Bài 24*: Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm ở ngoài phạm vi tờ giấy (hình...






{"content1": "a) Những cặp góc so le trong là $N1$ và $M2$, $M1$ và $N2$. Những cặp góc động vị là $N1$ và $N3$, $M1$ và $M3$.","content2": "b) Góc $M3 = 50^{\circ}$ nên góc $N3 = 50^{\circ}$ do a//b. Vì góc so le bên cạnh nhau bù nhau nên $N2 = 50^{\circ}$. Ta có $N1 + N2 + N3 = 180^{\circ}$ nên $N1 = 80^{\circ}$. Tương tự, $M1 = 80^{\circ}$.","content3": "Do đó, số đo mỗi góc còn lại của đỉnh M và N là $N1 = 80^{\circ}$ và $M1 = 80^{\circ}$.","content4": "Ngoài ra, ta cũng có $N2 = 50^{\circ}$ và $N3 = 50^{\circ}$.","content5": "Tổng số đo các góc của một tam giác là $180^{\circ}$.","content6": "Vậy ta đã tìm được số đo của mỗi góc còn lại."}