Bài 23: Quan sát hình 35, biết xx'//yy'//zz'. Chứng tỏ...
Câu hỏi:
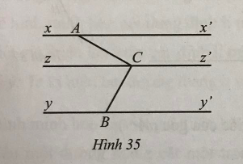
Bài 23: Quan sát hình 35, biết xx'//yy'//zz'. Chứng tỏ $\widehat{ACB}=\widehat{CAx'}+\widehat{CBy'}$
Câu trả lời:
Người trả lời: GV. Đỗ Văn Linh
Cách làm:Do xx'//zz' nên góc ACz và góc CAx' là hai góc đối nhau nên bằng nhau (hai góc so le trong).Tương tự, do yy'//zz' nên góc BCz và góc CBy' là hai góc đối nhau nên bằng nhau (hai góc so le trong).Vì hai góc ACz và BCz là hai góc kề nhau nên tổng của chúng chính là góc ACB.Từ đó, suy ra được $\widehat{ACB}=\widehat{CAx'}+\widehat{CBy'}$.Câu trả lời: Theo tính chất của góc đối nhau và góc kề nhau, ta có:$\widehat{ACz}=\widehat{CAx'}$ (hai góc so le trong) và $\widehat{BCz}=\widehat{CBy'}$ (hai góc so le trong).Vì hai góc ACz và BCz là hai góc kề nhau nên $\widehat{ACB}=\widehat{ACz}+\widehat{BCz}=\widehat{CAx'}+\widehat{CBy'}$.Do đó, $\widehat{ACB}=\widehat{CAx'}+\widehat{CBy'}$.
Câu hỏi liên quan:
- BÀI TẬPBài 16: Quan sát hình 28, biết a//b, $\widehat{M3}=50^{\circ}$a) Nêu những cặp góc so le...
- Bài 17: Quan sát hình 29, biết a//b, $3\widehat{A1}=2\widehat{A2}$. Tìm số đo mỗi góc của đỉnh A và...
- Bài 18: Tìm số đo góc B1, B2, B3, B4 trong hình 30, biết m//n
- Bài 19: Quan sát hình 31, biết $\widehat{P3}=\widehat{Q1}=75^{\circ},\widehat{M3}=10...
- Bài 20: Tìm số đo x, y trong hình 32.
- Bài 21: Tìm số đo góc BCD trong hình 33.
- Bài 22. Quan sát hình 34, biết d1//d2 và góc tù tạo bởi đường thẳng a và đường thẳng d1 bằng 15...
- Bài 24*: Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm ở ngoài phạm vi tờ giấy (hình...






{ "content1": "Do xx'//yy'//zz' nên góc ACy' và góc CBA cùng chung với góc x' và y' nên góc ACy' = góc CBA.", "content2": "Góc ACB và góc ACy' cùng chung với góc x' nên góc ACB = góc ACy'.", "content3": "Góc ACB và góc CBA cùng chung với góc y' nên góc CBA = góc ACy'.", "content4": "Vậy góc ACB = góc ACy' + góc CBA.", "content5": "Để chứng minh $\widehat{ACB}=\widehat{CAx'}+\widehat{CBy'}$ cần sử dụng tính chất song song của các đường thẳng và quy tắc cộng góc của tam giác."}