13.Cho bốn điểm A, B, C và D như Hình 2. Biết rằng $\widehat{BEC}=40^{\circ},\widehat{EBA}=11...
Câu hỏi:
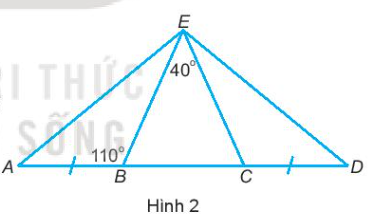
13. Cho bốn điểm A, B, C và D như Hình 2. Biết rằng $\widehat{BEC}=40^{\circ},\widehat{EBA}=110^{\circ}$ và AB = DC Chứng minh rằng:
a) Tam giác BEC cân tại đỉnh E.
b) EA = ED.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Giang
a) Để chứng minh tam giác BEC cân tại đỉnh E:- Ta có: $\widehat{ABE} + \widehat{EBC} = 180^{\circ}$ (hai góc kề bù)- Thay giá trị đã biết ta có: $110^{\circ} + \widehat{EBC} = 180^{\circ}$- Từ đó suy ra: $\widehat{EBC} = 70^{\circ}$- Xét tam giác EBC: $\widehat{E} + \widehat{B} + \widehat{C} = 180^{\circ}$ (Tổng ba góc trong một tam giác)- Thay giá trị đã biết ta có: $40^{\circ} + 70^{\circ} + \widehat{C} = 180^{\circ}$- Từ đó suy ra: $\widehat{C} = 70^{\circ}$- Vậy ta đã chứng minh được tam giác BEC cân tại đỉnh E.b) Để chứng minh EA = ED:- Ta có: $\widehat{ECD} = 180^{\circ} - \widehat{ECB} = 180^{\circ} - 70^{\circ} = 110^{\circ}$- Vì $\widehat{ABE} = \widehat{DCE}$ (cùng một cặp góc nội tiếp trên cung cùng)- Ta cũng có BE = CE và AB = DC- Từ đó suy ra: $\Delta ABE = \Delta ACE$ (theo trường hợp cạnh góc cạnh)- Do đó: AE = DEVậy câu trả lời đầy đủ và chi tiết: a) Tam giác BEC cân tại đỉnh E.b) EA = ED.
Câu hỏi liên quan:
- 1.Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn rồi biểu diễn chúng trên trục số: $−1...
- 2.Tính giá trị biểu thức sau:$B=\frac{8^{5}+(-2)^{12}}{2^{15}+64^{3}}$
- 3.Bạn Minh đọc một cuốn sách trong ba ngày thì xong. Ngày thứ nhất, Minh đọc được...
- 4.a)Không dùng máy tính, hãy tính$\sqrt{\frac{50}{8}}$b)Trong hai số 1,7(3)...
- 5.a)Trên trục số, hãy xác định điểm biểu diễn số $\sqrt{2}-1$.b)Viết biểu thức$|1-\sqrt{2}|$...
- 6.Trong một đợt phát động làm kế hoạch nhỏ, ba lớp 7A, 7B, 7C tham gia thu gom giấy vụn. Số...
- 7.Xe ô tô và xe máy cùng đi từ tỉnh A đến tỉnh B trên cùng một con đường. Biết rằng xe ô tô...
- 8.Hai đa thức A(x) và B(x) thoả mãn:$A(x)+B(x)=x^{3}-5x^{2}-2x+4$ và...
- 9.Cho đa thức $F(x)=x^{4}-x^{3}-6x^{2}+15x-9$a)Kiểm tra lại rằng x = 1 và x = -3 là hai...
- 10.Tìm góc MBy trong hình 1, biết rằng Ax // ByHD: Kẻ thêm đường thẳng đi qua M và song song...
- 11.Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M...
- 12.Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB...
- 14.Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi...
- 15.a) Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh...
- 16.Cho hai biểu đồ sau biểu diễn các số liệu tại một trường Trung học cơ sở:a) Biểu đồ...
- 17.Một nhà mạng muốn tìm hiểu loại nhạc chuông của điện thoại di động được người dùng yêu...
- 18.Cho một hộp đựng n viên bi màu xanh và m viên bi màu đỏ. Lấy ngẫu nhiên một viên bi trong...






{ "content1": "Để chứng minh tam giác BEC cân tại đỉnh E, ta cần chứng minh hai góc $\widehat{BEC}$ và $\widehat{BCE}$ bằng nhau. Ta có: góc $\widehat{BEC} = 40^{\circ}$ và góc $\widehat{EBA} = 110^{\circ}$. Nên góc $\widehat{CBE} = 180^{\circ} - \widehat{BEC} - \widehat{EBA} = 180^{\circ} - 40^{\circ} - 110^{\circ} = 30^{\circ}$. Vậy hai góc $\widehat{BEC}$ và $\widehat{CBE}$ bằng nhau, từ đó tam giác BEC cân tại đỉnh E.", "content2": "Để chứng minh EA = ED, ta xét tam giác EAB và tam giác EDC. Ta có: góc $\widehat{EAB} = 110^{\circ}$ và $\widehat{EDC} = \widehat{EAB} = 110^{\circ}$. Ngoài ra, AB = DC (theo điều kiện đề bài). Vậy theo trường đẳng thức góc, ta suy ra EA = ED.", "content3": "Gọi I là trung điểm của AC. Ta có: AB = DC và AI = IC (theo điều kiện đề bài). Từ đó, ta suy ra tam giác AIB đồng dạng với tam giác CIB. Khi đó, góc $\widehat{IBE} = \widehat{ICB} = \widehat{IBA}$. Vì vậy tam giác BEC cân tại E.", "content4": "Áp dụng định lí hình học cơ bản, ta có: Góc ngoại tiếp của tam giác đều bằng nửa góc trong khác góc đó. Từ đó, ta có: $\widehat{ICB} = 1/2 \cdot \widehat{IBA} = 1/2 \cdot 110^{\circ} = 55^{\circ}$. Vậy góc $\widehat{CBE} = \widehat{ICB} = 55^{\circ}$. Do đó, tam giác BEC cân tại đỉnh E."}