Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài 1 Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°
Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài 1
Trong bài này, chúng ta sẽ tìm hiểu về định lí côsin và định lí sin trong tam giác, cũng như giá trị lượng giác của một góc từ 0° đến 180°. Bài toán này được trích từ trang 70 của sách bài tập (SBT) toán lớp 10 "Cánh diều", được biên soạn theo chương trình đổi mới của Bộ Giáo dục.
Qua phần hướng dẫn giải, chúng ta sẽ hiểu rõ hơn về các khái niệm cơ bản của toán học, cụ thể là về lượng giác trong tam giác. Hướng dẫn chi tiết và cụ thể giúp học sinh dễ dàng nắm bắt bài học, từ đó cải thiện kỹ năng giải bài toán của mình.
Với việc áp dụng các kiến thức được hướng dẫn trong bài tập, học sinh sẽ rèn luyện được khả năng tư duy logic, phán đoán và giải quyết vấn đề, từ đó phát triển tư duy toán học và khả năng tự học hiệu quả. Hi vọng rằng thông qua việc giải bài tập này, học sinh sẽ có thêm niềm đam mê và sự tự tin khi học môn toán.
Bài tập và hướng dẫn giải
Bài 1: Cho 0° < α < 180°. Chọn câu trả lời đúng.
A. cosα < 0.
B. sinα > 0.
C. tanα < 0.
D. cotα > 0.
Bài 2 : Cho 0° < α, β < 180° và α + β = 180°. Chọn câu trả lời sai.
A. sinα + sinβ = 0.
B. cosα + cosβ = 0.
C. tanα + tanβ = 0.
D. cotα + cotβ = 0.
Bài 3 : Tính giá trị biểu thức
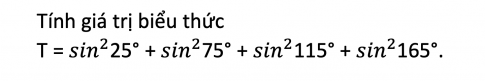
Bài 4 : 
Bài 5 : Cho tam giác ABC có AB = 6, AC = 8, A ̂=100°. Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Bài 6 : Cho tam giác ABC có B ̂ =60°, C ̂ =105° và BC = 15. Tính độ dài cạnh AC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng đơn vị).
Bài 7 : Cho tam giác ABC có AB = 5, AC = 7, BC = 9. Tính số đo góc A và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Bài 8 : Cho hình bình hành ABCD có AB = a, BC = b, AC = m, BD = n. Chứng minh: m2 + n2 = 2(a2 + b2).
Bài 9 : Từ một tấm tôn hình tròn có bán kính R = 1m, bạn Trí muốn cắt ra một hình tam giác ABC có các góc A = 45 độ, góc B = 75 độ. Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung AB, BC có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Bài 10: Một cây cao bị nghiêng so với mặt đất một góc 78 độ. Từ vị trí C cách gốc cây 20m, người ta tiến hành đo đạc và thu được kết quả góc ACB = 50 độ với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

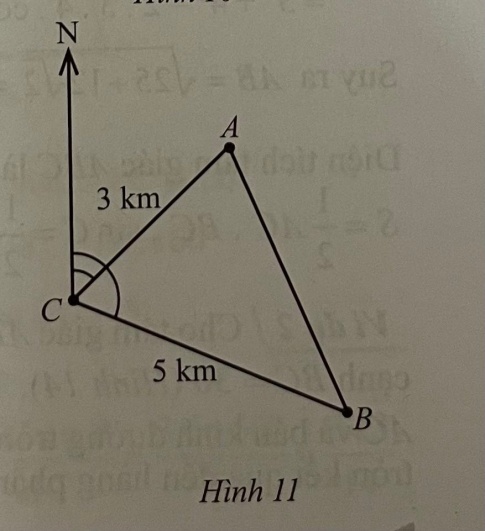
Bài 11 : Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C một khoảng 5km và lệch hướng bắc một góc 112,90° (Hình 11). Khoảng cách giữa hai tàu là bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng phần trăm).