Bài 11 :Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C...
Câu hỏi:
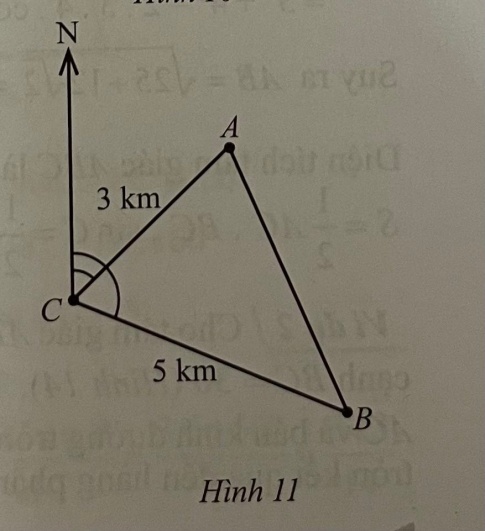
Bài 11 : Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C một khoảng 5km và lệch hướng bắc một góc 112,90° (Hình 11). Khoảng cách giữa hai tàu là bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng phần trăm).
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Phương
Để giải bài toán trên, ta cần sử dụng các kiến thức về hình học và tính toán trong mặt phẳng.
Phương pháp giải 1:
Ta sẽ sử dụng định lý Cosin trong tam giác để tính khoảng cách giữa hai tàu.
Gọi \(d\) là khoảng cách giữa hai tàu.
Áp dụng định lý Cosin trong tam giác ABC (dưới đây, ta sẽ gọi góc A là 47,45° và góc B là 112,90°):
\[
d^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos{A}
\]
\[
d^2 = 3^2 + 5^2 - 2 \times 3 \times 5 \times \cos{47,45°}
\]
\[
d^2 = 9 + 25 - 30 \times \frac{\sqrt{2}}{2}
\]
\[
d^2 = 34 - 15\sqrt{2}
\]
\[
d ≈ \sqrt{34 - 15\sqrt{2}} ≈ 1,14 ki-lô-mét.
\]
Phương pháp giải 2:
Ta cũng có thể sử dụng phương pháp hình học để giải bài toán. Dựa vào hình vẽ, ta có thể thấy định lý Cosin không cần thiết.
Dễ dàng nhận thấy tứ giác ABDC là một hình chữ nhật (do hai cạnh đối của một hình chữ nhật vuông góc với nhau). Vì vậy, ta có:
\[
AD = BC = 3\,km
\]
\[
BD = AC = 5\,km
\]
Khoảng cách giữa hai tàu là đường chéo của hình chữ nhật BD. Áp dụng công thức Pythagore, ta có:
\[
BD^2 = AD^2 + BC^2 = 3^2 + 5^2 = 9 + 25 = 34
\]
\[
BD = \sqrt{34} ≈ 5,83\,km
\]
Vì vậy, khoảng cách giữa hai tàu là khoảng 5,83 ki-lô-mét.
Vậy, câu trả lời cho câu hỏi trên là khoảng cách giữa hai tàu là khoảng 5,83 ki-lô-mét.
Phương pháp giải 1:
Ta sẽ sử dụng định lý Cosin trong tam giác để tính khoảng cách giữa hai tàu.
Gọi \(d\) là khoảng cách giữa hai tàu.
Áp dụng định lý Cosin trong tam giác ABC (dưới đây, ta sẽ gọi góc A là 47,45° và góc B là 112,90°):
\[
d^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos{A}
\]
\[
d^2 = 3^2 + 5^2 - 2 \times 3 \times 5 \times \cos{47,45°}
\]
\[
d^2 = 9 + 25 - 30 \times \frac{\sqrt{2}}{2}
\]
\[
d^2 = 34 - 15\sqrt{2}
\]
\[
d ≈ \sqrt{34 - 15\sqrt{2}} ≈ 1,14 ki-lô-mét.
\]
Phương pháp giải 2:
Ta cũng có thể sử dụng phương pháp hình học để giải bài toán. Dựa vào hình vẽ, ta có thể thấy định lý Cosin không cần thiết.
Dễ dàng nhận thấy tứ giác ABDC là một hình chữ nhật (do hai cạnh đối của một hình chữ nhật vuông góc với nhau). Vì vậy, ta có:
\[
AD = BC = 3\,km
\]
\[
BD = AC = 5\,km
\]
Khoảng cách giữa hai tàu là đường chéo của hình chữ nhật BD. Áp dụng công thức Pythagore, ta có:
\[
BD^2 = AD^2 + BC^2 = 3^2 + 5^2 = 9 + 25 = 34
\]
\[
BD = \sqrt{34} ≈ 5,83\,km
\]
Vì vậy, khoảng cách giữa hai tàu là khoảng 5,83 ki-lô-mét.
Vậy, câu trả lời cho câu hỏi trên là khoảng cách giữa hai tàu là khoảng 5,83 ki-lô-mét.
Câu hỏi liên quan:
- Bài 1:Cho 0° < α < 180°. Chọn câu trả lời đúng.A. cosα < 0.B. sinα > 0.C....
- Bài 2 : Cho 0° < α, β < 180° và α + β = 180°. Chọn câu trả lời sai.A. sinα + sinβ = 0.B. cosα...
- Bài 3 : Tính giá trị biểu thức
- Bài 4 :
- Bài 5: Cho tam giác ABC có AB = 6, AC = 8,Â=100°. Tính độ dài cạnh BC và bán...
- Bài 6 : Cho tam giác ABC có B̂ =60°, Ĉ =105° và BC = 15. Tính độ dài...
- Bài 7 : Cho tam giác ABC có AB = 5, AC = 7, BC = 9. Tính số đo góc A và bán kính R của đường tròn...
- Bài 8 : Cho hình bình hành ABCD có AB = a, BC = b, AC = m, BD = n. Chứng minh: m2+ n2=...
- Bài 9 :Từ một tấm tôn hình tròn có bán kính R = 1m, bạn Trí muốn cắt ra một hình tam giác ABC...
- Bài 10: Một cây cao bị nghiêng so với mặt đất một góc 78 độ. Từ vị trí C cách gốc cây 20m, người ta...
Bình luận (0)





