Bài tập 5 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Có ba hình hộp chữ nhật A, B, C...
Câu hỏi:
Bài tập 5 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng và thể tích được cho như Hình 2. Hình B và C có các kích thước giống nhau, hình A có cùng chiều rộng với B và C
a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị chúng bằng các phân thức cùng mẫu số.
b) Tính tổng chiều cao của hình A và C, chênh lệch chiều cao của hình A và B
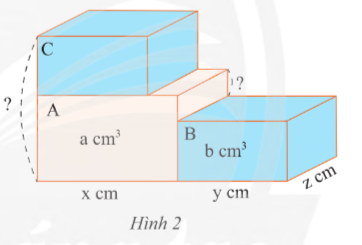
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
Phương pháp giải:
Để giải bài toán này, ta cần sử dụng các phương pháp tính toán căn bản về thể tích hình hộp chữ nhật và cũng cần áp dụng kiến thức về phân số.
Để tính chiều cao của các hình hộp chữ nhật, ta sẽ sử dụng công thức: Chiều cao = Thể tích / Diện tích đáy.
1. Tính chiều cao của hình B:
Đặt chiều cao của hình B là x (cm)
Vậy thể tích của hình B được biểu diễn bằng: V = bx = yz
Do đó, ta có: x = yz/b = bx/yz (cm)
2. Tính chiều cao của hình A:
Đặt chiều cao của hình A là y (cm)
Vậy thể tích của hình A được biểu diễn bằng: V = ay = xz
Do đó, ta có: y = xz/a = ay/xz (cm)
3. Tính chiều cao của hình C:
Vì hình C có các kích thước giống nhau với hình B, nên chiều cao của hình C cũng bằng: x = bx/yz (cm)
4. Tính tổng chiều cao của hình A và C:
Tổng chiều cao của hình A và C là: x + y = bx/yz + ay/xz = (bx + ay) / xyz (cm)
5. Chênh lệch chiều cao của hình A và B:
Chênh lệch chiều cao của hình A và B là: y - x = ay/xz - bx/yz = (ay - bx) / xyz (cm)
Câu trả lời:
a) Chiều cao hình B là: $\frac{bx}{yz}$ (cm)
Chiều cao hình A là: $\frac{ay}{xz}$ (cm)
Chiều cao hình C là: $\frac{bx}{yz}$ (cm)
b) Tổng chiều cao hình A và C là: $\frac{bx+ay}{xyz}$ (cm)
Chênh lệch chiều cao của hình A và B là: $\frac{ay-bx}{xyz}$ (cm)
Để giải bài toán này, ta cần sử dụng các phương pháp tính toán căn bản về thể tích hình hộp chữ nhật và cũng cần áp dụng kiến thức về phân số.
Để tính chiều cao của các hình hộp chữ nhật, ta sẽ sử dụng công thức: Chiều cao = Thể tích / Diện tích đáy.
1. Tính chiều cao của hình B:
Đặt chiều cao của hình B là x (cm)
Vậy thể tích của hình B được biểu diễn bằng: V = bx = yz
Do đó, ta có: x = yz/b = bx/yz (cm)
2. Tính chiều cao của hình A:
Đặt chiều cao của hình A là y (cm)
Vậy thể tích của hình A được biểu diễn bằng: V = ay = xz
Do đó, ta có: y = xz/a = ay/xz (cm)
3. Tính chiều cao của hình C:
Vì hình C có các kích thước giống nhau với hình B, nên chiều cao của hình C cũng bằng: x = bx/yz (cm)
4. Tính tổng chiều cao của hình A và C:
Tổng chiều cao của hình A và C là: x + y = bx/yz + ay/xz = (bx + ay) / xyz (cm)
5. Chênh lệch chiều cao của hình A và B:
Chênh lệch chiều cao của hình A và B là: y - x = ay/xz - bx/yz = (ay - bx) / xyz (cm)
Câu trả lời:
a) Chiều cao hình B là: $\frac{bx}{yz}$ (cm)
Chiều cao hình A là: $\frac{ay}{xz}$ (cm)
Chiều cao hình C là: $\frac{bx}{yz}$ (cm)
b) Tổng chiều cao hình A và C là: $\frac{bx+ay}{xyz}$ (cm)
Chênh lệch chiều cao của hình A và B là: $\frac{ay-bx}{xyz}$ (cm)
Câu hỏi liên quan:
- 1. Cộng, trừ hai phân thức cùng mẫuThực hành 1 trang 32 sách giáo khoa (SGK) toán lớp 8 tập 1...
- 2. Cộng, trừ hai phân thức khác mẫuThực hành 2 trang 34 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Thực hành 3 trang 34 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện phép tính...
- Vận dụng trang 34 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Viết biểu thức tính tổng thời gian đi...
- Bài tậpBài tập 1 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện các phép cộng, trừ...
- Bài tập 2 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Thực hiện các phép cộng, trừ...
- Bài tập 3 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện các phép tính sau:a)...
- Bài tập 4 trang 35 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cùng đi từ A đến thành phố B cách...
- Khởi động trang 31 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tại một cuộc đua thuyền diễn ra...
- Khám phá 1 trang 31 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Một hình chữ nhật lớn được...
- Khám phá 2 trang 32 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hai phân thức...






Do đó, ta có thể kết luận rằng chiều cao của các hình hộp chữ nhật A, B, C đều bằng nhau và có thể biểu diễn chúng bằng phân thức x/x, tổng chiều cao của hình A và C là 2x và chênh lệch chiều cao của hình A và B là 0.
Tổng chiều cao của hình A và C là hA + hC = x + x = 2x. Chênh lệch chiều cao của hình A và B là |hA - hB| = |x - x| = 0.
Chiều cao của hình hộp chữ nhật A, B, C lần lượt là hA, hB, hC. Theo điều kiện đề bài, ta có hA = hB và hB = hC. Giả sử chiều cao của mỗi hình hộp chữ nhật là x, ta có thể biểu diễn chiều cao của từng hình hộp theo phân thức là hA = x, hB = x, hC = x.