Bài tập 3.Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:a....
Câu hỏi:
Bài tập 3. Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
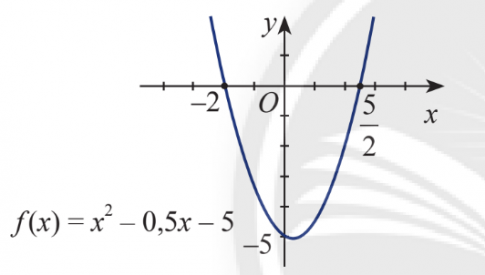
a. ${{x}^{2}}-0,5x-5\le 0$
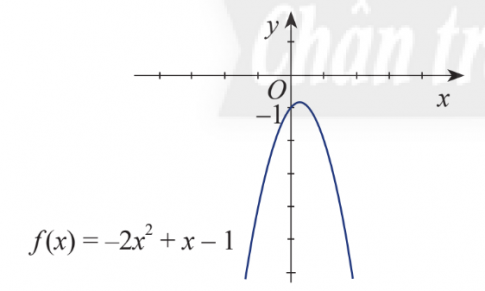
b. $-2{{x}^{2}}+x-1>0$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
a. Cách làm 1:- Để giải bất phương trình ${{x}^{2}}-0,5x-5\le 0$, ta cần xác định đồ thị của hàm số $y=x^2-0,5x-5$ trước.- Đồ thị của hàm số này sẽ là một đường parabol mở hướng lên.- Ta cần tìm các điểm cắt của đồ thị với trục hoành bằng cách giải phương trình $x^2-0,5x-5=0$.- Từ đó xác định được vùng giá trị mà bất phương trình thỏa mãn.b. Cách làm 2:- Đối với bất phương trình $-2{{x}^{2}}+x-1>0$, ta có thể chuyển về dạng $-2{{x}^{2}}+x-1\ge 0$ và xác định đồ thị của hàm số tương ứng.- Dựa vào đồ thị, ta xác định được vùng giá trị của x mà bất phương trình không thỏa mãn.Câu trả lời:a. Từ đồ thị $\Rightarrow$ ${{x}^{2}}-0,5x-5\le 0$ $\Leftrightarrow x\in \left[ -2;\frac{5}{2} \right]$Vậy bất phương trình có nghiệm $x\in \left[ -2;\frac{5}{2} \right]$b. Từ đồ thị $\Rightarrow$ Không tồn tại giá trị của x để $-2{{x}^{2}}+x-1>0$Vậy bất phương trình vô nghiệm.
Câu hỏi liên quan:
- Bài tập 4.Giải các phương trình sau:a. $\sqrt{{{x}^{2}}-7x}=\sqrt{-9{{x}^{2}}-8x+3}$b....
- Bài tập 5.Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8 cm. Tính độ dài của...
- Bài tập 6.Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30m/s. Khoảng...
- Bài tập 7.Một chú cá heo nhảy lên khỏi mặt nước. Độ cao h (mét) của chú cá heo so với mặt...
- Bài tập 8.Lợi nhuận một tháng p(x) của một quán ăn phụ thuộc vào giá trị trung bình x của các...
- Bài tập 9.Quỹ đạo của một quả bóng được mô tả bằng hàm số:$y=f(x)=-0,03{{x}^{2}}+0,4x+1,5$với...






{ "content1": "Để giải bất phương trình ${{x}^{2}}-0,5x-5\le 0$, ta cần xác định đồ thị của hàm số bậc hai $y={{x}^{2}}-0,5x-5$.", "content2": "Xét hàm số $y={{x}^{2}}-0,5x-5$ ta có đỉnh của parabol là điểm $D(-\frac{-0,5}{2},-5)=(-\frac{1}{4},-5)$", "content3": "Vì đồ thị mở lên nên ta chỉ cần xét xem đồ thị nằm dưới trục hoành trong khoảng nào để giải bất phương trình được.", "content4": "Do đó, ta cần giải hệ phương trình $y={{x}^{2}}-0,5x-5=0$ để xác định được khoảng nằm dưới trục hoành.", "content5": "Từ đó, ta sẽ có được đáp án cuối cùng cho bất phương trình ${{x}^{2}}-0,5x-5\le 0$."}