Bài 8 trang 120 toán lớp 7 tập 2 CDCho tam giác ABC có O là giao điểm của ba đường trung trực. Qua...
Câu hỏi:
Bài 8 trang 120 toán lớp 7 tập 2 CD
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh:
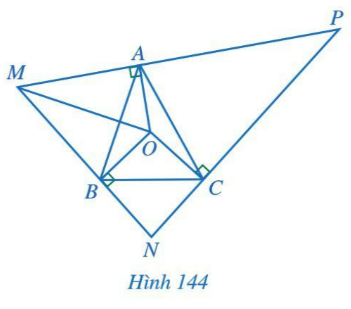
a. $\Delta OMA=\Delta OMB$
b. Tia MO là tia phân giác của góc NMP
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Long
Cách làm:1. Ta có OA = OB vì O là giao điểm của ba đường trung trực.2. Gọi I là giao điểm của MO và NP.3. Ta có $\widehat{MAO} = \widehat{MBO}$ vì MO là đường vằng của góc.4. Ta có $\widehat{NOI} = \widehat{MOI}$ vì I nằm trên đường phân giác góc NMP.5. Khi đó, ta có $\Delta OMA = \Delta OMB$.6. Vậy ta chứng minh được tia MO là tia phân giác của góc NMP.Câu trả lời: Vì O là giao điểm 3 đường trung trực, nên OA = OB.Gọi I là giao điểm của MO và NP.Suy ra $\widehat{MAO} = \widehat{MBO}$.Do đó, ta có tia MO là tia phân giác của góc NMP.
Câu hỏi liên quan:
- Bài 7 trang 119 toán lớp 7 tập 2 CDCho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng...
- Bài 9 trang 120 toán lớp 7 tập 2 CDBạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác...
- Bài 10 trang 120 toán lớp 7 tập 2 CDCho tam giác MNP có $\widehat{M}=40^{0}, \widehat{N}=70^{0}$....
- Bài 11 trang 120 toán lớp 7 tập 2 CDCho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc...
- Bài 12 trang 120 toán lớp 7 tập 2 CDCho tam giác nhọn MNP có trực tâm H. Khi đó góc HMN bằng góc...
- Bài 13 trang 120 toán lớp 7 tập 2 CDCho tam giác MNP có MN = 1dm, NP = 2dm, MP = x dm với x thuộc...
- Bài 14 trang 120 toán lớp 7 tập 2 CDNếu tam giác MNP có trọng tâm G, đường trung tuyến MI thì tỉ số...
Bình luận (0)





