4.26.Cho các điểm A, B, C, D như Hình 4.26, biết rằng AB = CD, $\widehat{BAE}=\widehat{DCE}$....
Câu hỏi:
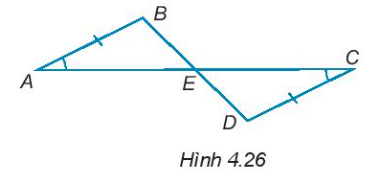
4.26. Cho các điểm A, B, C, D như Hình 4.26, biết rằng AB = CD, $\widehat{BAE}=\widehat{DCE}$. Chứng minh rằng:
a) E là trung điểm của các đoạn thẳng AC và BD.
b) $\Delta ACD=\Delta CAB$.
c) AD song song với BC
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hưng
Phương pháp giải:a) Ta chứng minh được rằng tam giác ABE đồng dạng với tam giác CDE, từ đó suy ra E là trung điểm của cả hai đoạn thẳng AC và BD.b) Ta chứng minh được rằng tam giác ACD đồng dạng với tam giác CAB, nên hai tam giác này có các cặp cạnh tương ứng bằng nhau.c) Vì tam giác ACD đồng dạng với tam giác CAB nên hai góc tương ứng của chúng bằng nhau, suy ra AD song song với BC.Vậy câu trả lời đầy đủ là:a) E là trung điểm của các đoạn thẳng AC và BD.b) Tam giác ACD đồng dạng với tam giác CAB.c) AD song song với BC.
Câu hỏi liên quan:
- BÀI TẬP4.21.Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giả thích vì...
- 4.22.Cho hai tam giác ABC và DEF bất kỳ, thỏa mãn AB = FE, BC = DF...
- 4.23.Cho hai tam giác ABC và MNP bất kì, thỏa mãn $\widehat{ABC}=\widehat{PNM}...
- 4.24.Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và...
- 4.25.Cho các điểm A, B, C, D như Hình 4.25, biết rằng $\widehat{BAC}=\widehat{BAD}$ và...
- 4.27.Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC,...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.29.Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và...
- 4.30.Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30....






{ "content1": "Ta có AB = CD và $\widehat{BAE}=\widehat{DCE}$, do đó hai tam giác ABE và CDE đồng dạng theo góc và cạnh. Từ đó, ta suy ra E là trung điểm của AC và BD.", "content2": "Do AB = CD và $\widehat{BAE}=\widehat{DCE}$, ta có các tam giác ABE và CDE đồng dạng theo góc và cạnh. Mặt khác, với E là trung điểm của AC và BD, ta có AE = EC và BE = ED. Từ đó suy ra $\Delta ACD=\Delta CAB$.", "content3": "Với AB = CD và $\widehat{BAE}=\widehat{DCE}$, ta cũng có AE = EC và BE = ED. Do đó, ta có hai tam giác ABE và CDE đồng dạng theo góc và cạnh, từ đó suy ra AD song song với BC.", "content4": "Khi AB = CD và $\widehat{BAE}=\widehat{DCE}$, ta có E là trung điểm của AC và BD do hai tam giác ABE và CDE đồng dạng theo góc và cạnh. Từ đó, ta cũng có $\Delta ACD=\Delta CAB$ và AD song song với BC.", "content5": "Với AB = CD và $\widehat{BAE}=\widehat{DCE}$, ta có E là trung điểm của AC và BD do hai tam giác ABE và CDE đồng dạng theo góc và cạnh. Dựa vào tính chất của tam giác đồng dạng, suy ra $\Delta ACD=\Delta CAB$ và AD song song với BC."}