4.24.Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và...
Câu hỏi:
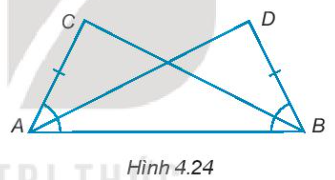
4.24. Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và $\widehat{DBA}=\widehat{CAB}$. Chứng minh rằng AD = BC.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đức
Để chứng minh rằng AD = BC, ta có thể giải theo các bước sau:
1. Vẽ đoạn thẳng CD.
2. Do AC = BD và $\widehat{DBA}=\widehat{CAB}$, nên $\Delta ABC$ và $\Delta BAD$ là hai tam giác cân.
3. Khi hai tam giác là tam giác cân và có 1 cặp cạnh bằng nhau, ta có thể kết luận rằng các cạnh tương ứng cũng bằng nhau.
4. Do đó, ta có AD = BC.
Vậy, câu trả lời cho câu hỏi "Chứng minh rằng AD = BC" là AD = BC.
1. Vẽ đoạn thẳng CD.
2. Do AC = BD và $\widehat{DBA}=\widehat{CAB}$, nên $\Delta ABC$ và $\Delta BAD$ là hai tam giác cân.
3. Khi hai tam giác là tam giác cân và có 1 cặp cạnh bằng nhau, ta có thể kết luận rằng các cạnh tương ứng cũng bằng nhau.
4. Do đó, ta có AD = BC.
Vậy, câu trả lời cho câu hỏi "Chứng minh rằng AD = BC" là AD = BC.
Câu hỏi liên quan:
- BÀI TẬP4.21.Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giả thích vì...
- 4.22.Cho hai tam giác ABC và DEF bất kỳ, thỏa mãn AB = FE, BC = DF...
- 4.23.Cho hai tam giác ABC và MNP bất kì, thỏa mãn $\widehat{ABC}=\widehat{PNM}...
- 4.25.Cho các điểm A, B, C, D như Hình 4.25, biết rằng $\widehat{BAC}=\widehat{BAD}$ và...
- 4.26.Cho các điểm A, B, C, D như Hình 4.26, biết rằng AB = CD, $\widehat{BAE}=\widehat{DCE}$....
- 4.27.Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC,...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.29.Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và...
- 4.30.Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30....






{
"content1": "Vì AC = BD và $\widehat{DBA}=\widehat{CAB}$, suy ra tam giác ABC và tam giác BDA(ABD) đều có 2 cạnh bằng nhau và một góc tương đương, nên theo định lý cạnh và góc bằng nhau, ta có AD = BC.",
"content2": "Ta có $\widehat{DBA}=\widehat{CAB}$ (cùng chắn qua cùng một dây) và AC = BD (đều bằng nhau), từ đó suy ra tam giác ABC và tam giác BDA(ABD) đồng dạng. Do đó, theo tính chất của tam giác đồng dạng, ta có AD = BC.",
"content3": "Vì AC = BD và $\widehat{DBA}=\widehat{CAB}$, ta có thể sử dụng định lý cạnh và góc bằng nhau trong tam giác. Như vậy, ta suy ra AD = BC bằng cách so sánh 2 tam giác ABC và BDA(ABD).",
"content4": "Gọi E là trung điểm của CD, khi đó tam giác ABC và tam giác BDE là tam giác cân cân, nên ta có AE = EB. Từ đó, ta có tam giác AED đồng dạng với tam giác BEC. Do đó, theo tính chất của tam giác đồng dạng, ta suy ra AD = BC."
}