4.25.Cho các điểm A, B, C, D như Hình 4.25, biết rằng $\widehat{BAC}=\widehat{BAD}$ và...
Câu hỏi:
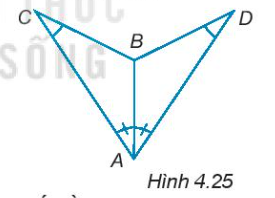
4.25. Cho các điểm A, B, C, D như Hình 4.25, biết rằng $\widehat{BAC}=\widehat{BAD}$ và $\widehat{BCA}=\widehat{BDA}$.
Chứng minh rằng $\Delta ABC = \Delta ABD.$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Giang
Phương pháp giải:Ta cần chứng minh rằng hai tam giác $\Delta ABC$ và $\Delta ABD$ bằng nhau.Dựa vào công thức góc trong tam giác, ta có:$\widehat{ABC} = 180^{\circ} - \widehat{BAC} - \widehat{BCA}$ (1)$\widehat{ABD} = 180^{\circ} - \widehat{BAD} - \widehat{BDA}$ (2)Và từ các giả thiết $\widehat{BAC} = \widehat{BAD}$ và $\widehat{BCA} = \widehat{BDA}$, suy ra $\widehat{ABC} = \widehat{ABD}$.Khi đó, ta có thể kết luận rằng hai tam giác $\Delta ABC$ và $\Delta ABD$ bằng nhau với hai góc tương ứng bằng nhau và cạnh chung là cạnh AB.Câu trả lời: $\Delta ABC = \Delta ABD$ (chứng minh góc góc cạnh).
Câu hỏi liên quan:
- BÀI TẬP4.21.Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giả thích vì...
- 4.22.Cho hai tam giác ABC và DEF bất kỳ, thỏa mãn AB = FE, BC = DF...
- 4.23.Cho hai tam giác ABC và MNP bất kì, thỏa mãn $\widehat{ABC}=\widehat{PNM}...
- 4.24.Cho các điểm A, B, C, D như Hình 4.24, biết rằng AC = BD và...
- 4.26.Cho các điểm A, B, C, D như Hình 4.26, biết rằng AB = CD, $\widehat{BAE}=\widehat{DCE}$....
- 4.27.Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC,...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.28.Cho tam giác ABC bằng tam giác DEF (H.4.28).a) Gọi M và N lần lượt là trung điểm các...
- 4.29.Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và...
- 4.30.Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30....






{ "content1": "Khi $\widehat{BAC}=\widehat{BAD}$ và $\widehat{BCA}=\widehat{BDA}$, ta có thể suy ra được $\angle ABD = \angle ABC$ (cùng bằng $\widehat{BAC}$) và $\angle ADB = \angle ACB$ (cùng bằng $\widehat{BCA}$).", "content2": "Do $\angle ABD = \angle ABC$ và $\angle ADB = \angle ACB$, nên theo góc - cạnh - góc, ta có $\Delta ABD = \Delta ABC$ (có cùng 2 cạnh và góc tương ứng bằng nhau).", "content3": "Vậy ta đã chứng minh được rằng $\Delta ABC = \Delta ABD$ khi có điều kiện $\widehat{BAC}=\widehat{BAD}$ và $\widehat{BCA}=\widehat{BDA}$."}