2.GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN BẰNG PHƯƠNG PHÁP GAUSSHoạt động 2: Hệ bậc nhất ba ẩn có dạng...
Câu hỏi:
2.GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN BẰNG PHƯƠNG PHÁP GAUSS
Hoạt động 2: Hệ bậc nhất ba ẩn có dạng tam giác
Cho hệ phương trình 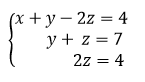
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
Để giải hệ phương trình bậc nhất ba ẩn bằng phương pháp Gauss, ta cần thực hiện các bước sau:Bước 1: Viết hệ phương trình dưới dạng ma trận mở rộng.Bước 2: Thực hiện các phép biến đổi hàng để đưa ma trận về dạng tam giác.Bước 3: Giải phương trình sau khi ma trận đã được đưa về dạng tam giác.Bước 4: Tìm ra nghiệm của hệ phương trình.Với hệ phương trình đã cho, ta có:\[\begin{cases}x + 2y + 3z = 6\\2x + y + z = 5\\3x + 3y - 2z = 2\end{cases}\]Viết hệ phương trình dưới dạng ma trận mở rộng:\[\begin{bmatrix}1 & 2 & 3 & \vert & 6\\2 & 1 & 1 & \vert & 5\\3 & 3 & -2 & \vert & 2\end{bmatrix}\]Thực hiện các phép biến đổi hàng để đưa ma trận về dạng tam giác:\[\begin{bmatrix}1 & 2 & 3 & \vert & 6\\0 & -3 & -5 & \vert & -7\\0 & 0 & 2 & \vert & 2\end{bmatrix}\]Từ phương trình cuối ta tính được z = 1. Thay z = 1 vào phương trình thứ hai ta được y = 2. Cuối cùng, thay y = 2 và z = 1 vào phương trình đầu tiên ta được x = 1.Vậy nghiệm của hệ phương trình là (x, y, z) = (1, 2, 1).
Câu hỏi liên quan:
- Khởi độngÔng An đầu tư 240 triệu đồng vào ba quỹ khác nhau: một phần trong quỹ thị trường tiền tệ...
- 1. KHÁI NIỆM HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨNVí dụ 1:Hệ phương trình nào dưới đây là hệ phương trình...
- Luyện tập 1. Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Kiểm tra xem ba số (-3;2;-1)...
- Luyện tập 2: Giải hệ phương trình
- Hoạt động 3. Giải hệ phương trình bậc nhất ba ẩn bằng phương pháp GaussCho hệ phương trìnha, Khử ẩn...
- Luyện tập 3: Giải các hệ phương trình saua, b, c,
- Vận dụng 1. Hà mua văn phòng phẩm cho nhóm bạn cùng lớp gồm Hà, Lan và Minh hết tổng cộng 820 nghìn...
- 3. TÌM NGHIỆM CỦA HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN BẰNG MÁY TÍNHLuyện tập 4. Sử dụng máy tính cầm tay...
- Vận dụng 2:Tại một quốc gia khoảng 400 loài động vậtnằm trong danh sách các loài có...
- Bài tập1.1. Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Kiêm rtra xem bộ ba số (2;0...
- 1.2. Giải các hệ phương trình sau:a,b,
- 1.3. Giải các hệ phương trình sau bằng phương pháp Gauss
- 1.4.Ba người cùng làm việc cho một công ty với vị trí lần lượt là quản lí kho, quản lí văn...
- 1.5. Năm ngoái, người ta có thể mua ba mẫu xe ôtô của ba hãng X, Y, Z với tổng số tiền là 2,8 tỉ...
- 1.6. Cho hệ phương trình bậc nhất ba ẩn sau:a, Giả sử (Xo;Yo;Zo) Và (X1;Y1;Z1) là hai nghiệm...
Bình luận (0)





