Người trả lời: GV. Đỗ Đăng Giang
Phương pháp giải:a) Ta có:- Hai góc đối đỉnh: $\widehat{F1} = \widehat{F2}$- Hai cạnh đối xứng: $FB = FC$- Hai góc so le trong: $\widehat{FBA} = \widehat{FCK}$ (do AB // CD)Do đó, ta có $\Delta FBA = \Delta FCK$ (theo điều kiện góc - cạnh - góc).b) Ta đã chứng minh được $\Delta FBA = \Delta FCK$, nên $FA = FK$. Xét tam giác ADK, ta thấy EA = ED và FA = FK, suy ra EF là đường trung bình của tam giác ABC nên EF // DK.Với AB // CD suy ra EF // CD // AB.c) Ta đã chứng minh rằng EF // AB và EF // CD, nên EF // AB // CD.Như vậy, EF chính là đường trung bình của tam giác ADK, nên ta có $EF = \frac{1}{2}DK = \frac{1}{2}(CD + CK)$.Và do CK = BA (do $\Delta FBA = \Delta FCK$), nên $EF = \frac{AB + CD}{2}$.Vậy, câu trả lời cho câu hỏi trên là:a) Tam giác FBA và tam giác FCK có bằng nhau vì chúng có cùng một cặp góc và cạnh đồng dạng.b) EF // CD // AB.c) $EF = \frac{AB + CD}{2}$.
![]() Khổng Trường
Khổng Trường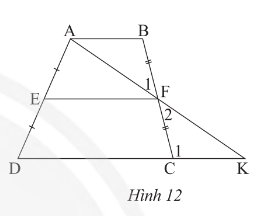
![]() Khổng Trường
Khổng Trường![]() Vũ Gia Hân
Vũ Gia Hân![]() nguyễn thị thùy linh
nguyễn thị thùy linh