1. Đường trung bình của tam giácHoạt động khám phá 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2...
Câu hỏi:
1. Đường trung bình của tam giác
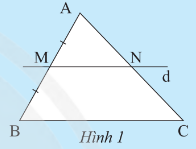
Hoạt động khám phá 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Đạt
Phương pháp giải:Ta có tam giác ABC với đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N. Khi đó, theo định lí Thales, ta có:$\frac{AM}{AB} = \frac{AN}{AC} = \frac{1}{2}$Vậy, ta có $AN = \frac{1}{2}AC$, tức N chính là trung điểm của AC.Câu trả lời: N là trung điểm của AC.
Câu hỏi liên quan:
- Hoạt động khởi động trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Giữa hai điểm B và C có...
- Thực hành 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài đoạn thẳng NQ trong...
- Vận dụng 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 5, chứng minh MN là...
- 2. Tính chất của đường trung bìnhHoạt động khám phá 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập...
- Thực hành 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 8, cho biết JK = 10 cm,...
- Vận dụng 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính khoảng cách BC trong phần...
- Bài tậpBài tập 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho MN là đường trung bình...
- Bài tập 2 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài đoạn PQ (Hình 10)
- Bài tập 3 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho biết cạnh mỗi ô vuông bằng 1 cm....
- Bài tập 4 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB //CD) có E...
- Bài tập 5 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC nhọn. Gọi M, N, P...
- Bài tập 6 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Một mái nhà được vẽ lại như Hình 13....
- Bài tập 7 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Ảnh chụp từ Google Maps của một...






Chứng minh bằng phương pháp theo quan sát: Quan sát hình vẽ, ta thấy đường thẳng d cắt cạnh AC tại N sao cho cả hai phần AC được chia thành hai phần bằng nhau. Do đó, N chính là trung điểm của AC trong tam giác ABC.
Áp dụng phép phân giữa: Đặt AM = a, MB = a, AC = b, CN = x. Áp dụng phép phân giữa ta có: AN = NC = x. Suy ra N là trung điểm của AC.
Chứng minh bằng phương pháp tương tự: Ta có thể chứng minh bằng cách sử dụng các định lí về vị trí tương đối giữa các đường thẳng trong tam giác, tính chất của trung điểm và tính chất của tam giác. Điều này cũng dẫn đến kết luận rằng N là trung điểm của AC.
Sử dụng tính chất song song: 'Hai đường thẳng song song khi và chỉ khi chúng có cùng một vector chỉ phương'. Vì d dưới đồng bộ với cạnh BC, nên d cũng song song với BC. Do đó, đường d cắt AC tại N sẽ chia đoạn AC thành hai phần bằng nhau, từ đó suy ra N là trung điểm của AC.
Áp dụng định lí trung điểm: 'Đường chứa đoạn nối giữa một đỉnh của tam giác và trung điểm của cạnh đối diện với đỉnh đó chia đoạn đó thành hai phần bằng nhau'. Với trường hợp này, ta có trung điểm M của cạnh AB và đỉnh C của tam giác ABC, nên N là trung điểm của AC.